
分析 方法1:利用放缩法进行证明即可.
方法2:利用等价转化法进行证明.
解答 证明:法(1)f(x)=$\sqrt{1+{x}^{2}}$,
则|f(a)-f(b)|=|$\sqrt{1+{a}^{2}}$-$\sqrt{1+{b}^{2}}$|=$\frac{|1+{a}^{2}-(1+{b}^{2})|}{\sqrt{1+{a}^{2}}+\sqrt{1+{b}^{2}}}$=$\frac{|{a}^{2}-{b}^{2}|}{\sqrt{1+{a}^{2}}+\sqrt{1+{b}^{2}}}$
=$\frac{|(a-b)(a+b)|}{\sqrt{1+{a}^{2}}+\sqrt{1+{b}^{2}}}$≤$\frac{|a-b|(|a|+|b|)}{\sqrt{1+{a}^{2}}+\sqrt{1+{b}^{2}}}$≤$\frac{|a-b|(|a|+|b|)}{|a|+|b|}$=|a-b|.
法(2)|f(a)-f(b)|≤|a-b|?|f(a)-f(b)|2≤|a-b|2?f2(a)+f2(b)-2f(a)f(b)≤a2+b2-2ab
?1+a2+1+b2-2$\sqrt{1+{a}^{2}}$•$\sqrt{1+{b}^{2}}$≤a2+b2-2ab?1+ab≤$\sqrt{1+{a}^{2}}$•$\sqrt{1+{b}^{2}}$,
当1+ab<0时,上式成立.
当1+ab≥0时,上式等价于 1+a2b2+2ab≤(1+a2)(1+b2)=1+a2b2+a2+b2?2ab<a2+b2?(a-b)2≥0,
∵(a-b)2≥0恒成立.
∴|f(a)-f(b)|≤|a-b|.
点评 本题主要考查不等式的证明,利用放缩法以及等价转化法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
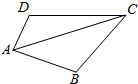 如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.
如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com