
【题目】已知点的序列An(xn,0),n∈N*,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……,An是线段An-2An-1的中点,……
(1)写出xn与xn-1,xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)根据题意,An是线段An﹣2An﹣1的中点,可得xn与xn﹣1、xn﹣2之间的关系式,
(2)由题意知a1=a,a2=﹣![]() a,a3=
a,a3=![]() a,由此推测:an=(﹣
a,由此推测:an=(﹣![]() )n﹣1a(n∈N*)再进行证明.
)n﹣1a(n∈N*)再进行证明.
详解:(1)当n≥3时,xn![]()
(2)a1=x2-x1=a,
a2=x3-x2![]()
=![]()
a3=x4-x3![]()
=![]()
由此推测数列{an}的通项公式为an![]() ∈N*).
∈N*).
用数学归纳法证明:
①当n=1时,a1=x2-x1=a![]() .
.
②假设当n=k(k∈N*,且k≥1)时,猜测成立,
即ak![]() n=k+1时,
n=k+1时,
ak+1=xk+2-xk+1![]() =
=![]()
=![]()
![]() .
.
根据①和②可知,对任意n∈N*,猜测an![]() ∈N*)成立,即数列{an}的通项公式为an
∈N*)成立,即数列{an}的通项公式为an![]() ∈N*).
∈N*).


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.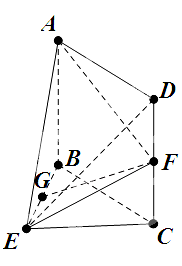
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是
是两个不同平面,则下列命题正确的是
A.若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B.若m,n平行于同一平面,则m与n平行
C.若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D.若m,n不平行,则m与n不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1:![]() 过点P且离心率为
过点P且离心率为 ![]() .
.

(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为![]() 元/kWh,年用电量为
元/kWh,年用电量为![]() kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为![]() ),该地区电力的成本价为0.30元/ kWh.
),该地区电力的成本价为0.30元/ kWh.
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 之间的函数关系式;
之间的函数关系式;
(2)设![]() =
=![]() ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上的一点与两个焦点构成的三角形周长为
,且椭圆上的一点与两个焦点构成的三角形周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求
,求![]() 的值;
的值;
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若是,求点
为定值?若是,求点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①命题“若a=0,则ab=0”的否命题是“若a=0,则ab≠0”;
②已知命题p:x∈R,x2+6x+11<0,则![]() p:x∈R,x2+6x+11≥0;
p:x∈R,x2+6x+11≥0;
③若命题“![]() p”与命题“p或q”都是真命题,则命题q一定是真命题;
p”与命题“p或q”都是真命题,则命题q一定是真命题;
④命题“若0<a<1,则loga(a+1)<log![]()
其中正确结论的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=logax(a>0且a≠1)的图象过点(4,2),
(1)求a的值.
(2)若g(x)=f(1-x)+f(1+x),求g(x)的解析式及定义域.
(3)在(2)的条件下,求g(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com