
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 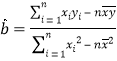 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知点
.已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在
在![]() 上,
上, ![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)求![]() 的值;
的值;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,当过点
,当过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点时,
两点时, ![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行;
B. 若两个平面平行,则分别位于这两个平面的直线也互相平行;
C. 平行于同一个平面的两个平面平行;
D. 若两个平面平行,则其中一个平面内的直线平行于另一个平面;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在![]() 岁到
岁到![]() 岁的人群中随机调查了
岁的人群中随机调查了![]() 人,并得到如图所示的频率分布直方图,在这
人,并得到如图所示的频率分布直方图,在这![]() 人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:
人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:

年龄 | 不支持“延迟退休年龄政策”的人数 |
|
|
|
|
|
|
|
|
|
|
(1)由频率分布直方图,估计这![]() 人年龄的平均数;
人年龄的平均数;
(2)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以
的前提下,认为以![]() 岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
附:![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数①![]() ,②
,②![]() ,③
,③![]() ,
,
判断如下两个命题的真假:
命题甲: ![]() 在区间
在区间![]() 上是增函数;
上是增函数;
命题乙: ![]() 在区间
在区间![]() 上恰有两个零点
上恰有两个零点![]() ,且
,且![]() .
.
能使命题甲、乙均为真的函数的序号是
A. ① B. ② C. ①③ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 的焦点为F,
的焦点为F,![]() 是抛物线E上一点,且
是抛物线E上一点,且![]() .
.
![]() 1
1![]() 求抛物线E的标准方程;
求抛物线E的标准方程;
![]() 2
2![]() 设点B是抛物线E上异于点A的任意一点,直线AB与直线
设点B是抛物线E上异于点A的任意一点,直线AB与直线![]() 交于点P,过点P作x轴的垂线交抛物线E于点M,设直线BM的方程为
交于点P,过点P作x轴的垂线交抛物线E于点M,设直线BM的方程为![]() ,k,b均为实数,请用k的代数式表示b,并说明直线BM过定点.
,k,b均为实数,请用k的代数式表示b,并说明直线BM过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如下的列联表:

随机变量![]() 经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C. 有97.5%以上的把握认为“爱好该项运动与性别有关”
D. 有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com