练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （本小题满分10分）
    从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭7次，命中的环数如下：
    甲
    		10
    		8
    		6
    		9
    		7
    		6
    		10
    乙
    		10
    		9
    		8
    		6
    		7
    		8
    		8
    （1）计算甲、乙两人射箭命中环数的平均数和方差；
    （2）比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．
    ="8" ，="8" ；
     ，． 从成绩的稳定性考虑，选择乙参赛更合适
    解：（1）计算得：="8" ，="8"
     ，． 　        ………5分学
    （2）由（1）可知，甲、乙两名学生射箭命中环数的平均数相等，
    但>，这表明乙的成绩比甲更稳定一些．
    从成绩的稳定性考虑，选择乙参赛更合适．…………10分学
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分13分）
    某零售店近五个月的销售额和利润额资料如下表：
    商店名称
    		A
    		B
    		C
    		D
    		E
    E
    销售额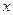 (千万元)
    		3
    		5
    		6
    		7
    		9
    9
    利润额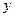(百万元)
    		2
    		3
    		3
    		4
    		5
    （1）画出散点图．观察散点图，说明两个变量有怎样的相关关系；
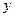    （2）用最小二乘法计算利润额关于销售额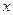的回归直线方程；
    （3）当销售额为4(千万元)时，利用（2）的结论估计该零售店的利润额（百万元）.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    为了考察两个变量x和y之间的线性相关性，甲、乙两个同学各自独立地做了10次试验和15次试验，并且利用线性回归方法，求得回归直线分别为l1和l2，已知两个人在试验中发现对变量x的观测数据的平均数都为s，对变量y的观测数据平均数都为t，那么下列说法正确的是（　　）
    A．l1和l2有交点(s,t)B．l1和l2相交，但交点不一定是(s,t)
    C．l1和l2必平行D．l1和l2必重合

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    一位母亲记录了儿子3～9岁的身高，由此建立的身高与年龄的回归模型为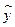=" 7.19" x +73.93. 用这个模型预测这个孩子10岁时的身高，则正确的叙述是（ ）
    A．身高一定是145.83 cm；B．身高在145.83 cm以上；
    C．身高在145.83 cm以下；D．身高在145.83 cm左右.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

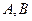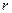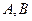    甲乙丙丁四位同学各自对两变量的线性相关性进行分析，并用回归分析方法得到相关系数与残差平方和，如右表则哪位同学的试验结果体现两变量更强的线性相关性（   ）
     
    		甲
    		乙
    		丙
    		丁










     
    A 甲            B 乙          C 丙          D 丁

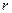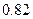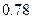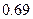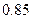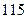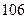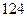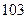    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

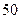    某经济研究小组对全国个中小城市进行职工人均工资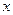与居民人均消费水平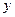进行了统计调查，发现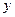与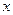具有相关关系，其回归方程为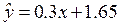（单位：千元）．某城市居民人均消费水平为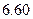，估计该城市职工人均消费水平额占居民人均工资收入的百分比为
    A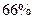．B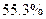．C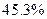．D．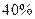

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知某班4个小组的人数分别为10、10、x、8，这组数据的中位数是____

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）已知x，y之间的一组数据如下表： 
    x
    		1
    		3
    		6
    		7
    		8
    y
    		1
    		2
    		3
    		4
    		5
    （1）以x为横坐标，y为纵坐标在直角坐标系中画出散点图，并说明这两个变量之间的关系是正相关关系还是负相关关系。
    （2）求线性回归方程.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    观察两个相关变量的如下数据：

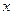    		－1
    		－2
    		－3
    		－4
    		－5
    		5
    		4
    		3
    		2
    		1

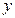    		－0.9
    		－2
    		－3.1
    		－3.9
    		－5.1
    		5
    		4.1
    		2.9
    		2.1
    		0.9
    则两个变量间的回归直线方程为 （   ）
    A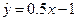．B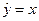．C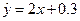．D．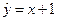

    查看答案和解析>>

    同步练习册答案