
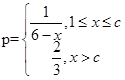 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.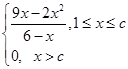 ;
;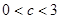 时,日产量为c万件时,可获得最大利润,当
时,日产量为c万件时,可获得最大利润,当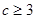 时,日产量为3万件时,可获得最大利润
时,日产量为3万件时,可获得最大利润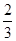 ,则T=
,则T=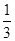 x×2-
x×2-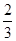 x×1=0. 当1≤x≤c时,P=
x×1=0. 当1≤x≤c时,P=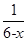 , 则T=(1-
, 则T=(1-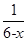 )x×2-(
)x×2-(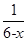 )x×1=
)x×1=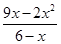 . 综上,日盈利额T(万元)与日产量x(万件)的函数关系为: T=
. 综上,日盈利额T(万元)与日产量x(万件)的函数关系为: T=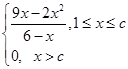 ; (2)由(1)知,当x>c时,每天的盈利额为0. 当1≤x≤c时,T=
; (2)由(1)知,当x>c时,每天的盈利额为0. 当1≤x≤c时,T=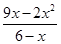 =15-2[(6-x)+
=15-2[(6-x)+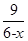 ].因c为小于6的正常数,故6-x>0,故T=15-2[(6-x)+
].因c为小于6的正常数,故6-x>0,故T=15-2[(6-x)+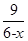 ]≤15-12=3, 当且仅当x=3时取等号. 综上,当
]≤15-12=3, 当且仅当x=3时取等号. 综上,当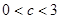 时,日产量为c万件时,可获得最大利润,当
时,日产量为c万件时,可获得最大利润,当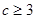 时,日产量为3万件时,可获得最大利润.
时,日产量为3万件时,可获得最大利润.

科目:高中数学 来源:不详 题型:解答题
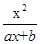 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.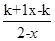 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 3 |
| 1 |
| 2 |
| A.A、B、C、D | B.B、C、A、D | C.B、A、C、D | D.C、A、B、D |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.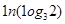 | B.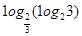 |
C.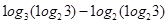 | D.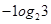 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
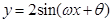 为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为
为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为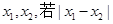 的最小值为π,则( )
的最小值为π,则( )A.ω=2,θ=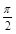 | B.ω=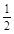 ,θ= ,θ=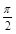 |
C.ω=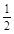 ,θ= ,θ=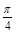 | D.ω=2,θ=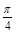 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com