
【题目】设函数f(x)=丨x+a+1丨+丨x-![]() 丨,(a>0)。
丨,(a>0)。
(1)证明:f(x)≥5;
(2)若f(1)<6成立,求实数a的取值范围。
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,![]() 和
和![]() 都是正三角形,
都是正三角形,![]() , E、F分别是AC、BC的中点,且PD⊥AB于D.
, E、F分别是AC、BC的中点,且PD⊥AB于D.
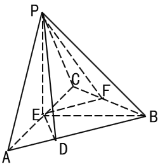
(Ⅰ)证明:直线![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,![]() 和
和![]() 都是正三角形,
都是正三角形,![]() , E、F分别是AC、BC的中点,且PD⊥AB于D.
, E、F分别是AC、BC的中点,且PD⊥AB于D.

(Ⅰ)证明:直线![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()
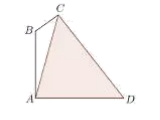
(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的通项公式为
的通项公式为![]() ,其中
,其中![]() ,
,![]() 、
、![]() .
.
(1)试写出一组![]() 、
、![]() 的值,使得数列
的值,使得数列![]() 中的各项均为正数.
中的各项均为正数.
(2)若![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,且对任意的
,且对任意的![]() (
(![]() ),均有
),均有![]() ,写出所有满足条件的
,写出所有满足条件的![]() 的值.
的值.
(3)若![]() ,数列
,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且使
,且使![]() (
(![]() 、
、![]() ,
,![]() )的
)的![]() 和
和![]() 有且仅有
有且仅有![]() 组,
组,![]() 、
、![]() 、…、
、…、![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,求
个连续项的值相等,其它项的值均不相等,求![]() 、
、![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为 an=(n﹣k1)(n﹣k2),其中k1,k2∈Z:
(1)试写出一组k1,k2∈Z的值,使得数列{an}中的各项均为正数;
(2)若k1=1、k2∈N*,数列{bn}满足bn=![]() ,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
(3)若0<k1<k2,数列{cn}满足cn=an+|an|,其前n项和为Sn,且使ci=cj≠0(i,j∈N*,i<j)的i和j有且仅有4组,S1、S2、…、Sn中至少3个连续项的值相等,其他项的值均不相等,求k1,k2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com