
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥底面ABCD,E在PB上.
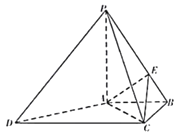
(1)证明:AC⊥PD;
(2)若PE=2BE,求三棱锥P﹣ACE的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过A作AF⊥DC于F,推导出AC⊥DA,AC⊥PA,从而AC⊥平面PAD,由此能求出AC⊥PD.
(2)由VP﹣ACE=VP﹣ABC﹣VE﹣ABC,能求出三棱锥P﹣ACE的体积.
(1)过A作AF⊥DC于F,
因为AB∥CD,AB⊥BC,AB=BC=1,所以CF=DF=AF=1,
所以∠DAC=90°,所以AC⊥DA,
又PA⊥底面ABCD,AC平面ABCD,所以AC⊥PA,
又PA,AD平面PAD,PA∩AD=A,所以AC⊥平面PAD,
又PD平面PAD,∴AC⊥PD.
(2)由PE=2BE,可得VP﹣ACE=VP﹣ABC﹣VE﹣ABC,
所以![]() ,
,![]() ,
,
所以三棱锥P﹣ACE的体积VP﹣ACE=VP﹣ABC﹣VE﹣ABC![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
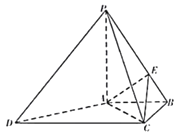
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
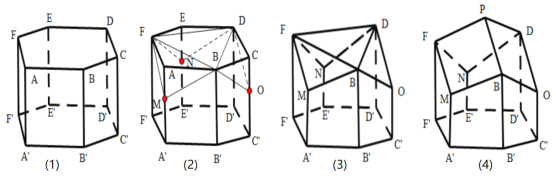
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为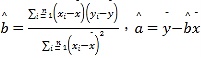
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“国”、“富”、“民”、“强”四个字,有放回地从中任取一张卡片,将三次抽取后“国”“富”两个字都取到记为事件A,用随机模拟的方法估计事件A发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“国”、“富”、“民”、“强”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
由此可以估计事件A发生的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD的底面是正方形,![]() 底面ABCD,
底面ABCD,![]() ,E是侧棱的中点.
,E是侧棱的中点.
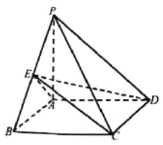
(1)求异面直线AE与PD所成的角;
(2)求点B到平面ECD的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面PAD是等边三角形,且平面
中,侧面PAD是等边三角形,且平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
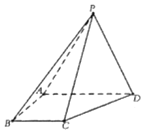
(1)AD上是否存在一点M,使得平面![]() 平面ABCD;若存在,请证明,若不存在,请说明理由;
平面ABCD;若存在,请证明,若不存在,请说明理由;
(2)若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
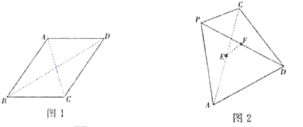
【题目】已知四边形![]() 是边长为5的菱形,对角线
是边长为5的菱形,对角线![]() (如图1),现以
(如图1),现以![]() 为折痕将菱形折起,使点
为折痕将菱形折起,使点![]() 达到点
达到点![]() 的位置.棱
的位置.棱![]() ,
,![]() 的中点分为
的中点分为![]() ,
,![]() ,且四面体
,且四面体![]() 的外接球球心落在四面体内部(如图2),则线段
的外接球球心落在四面体内部(如图2),则线段![]() 长度的取值范围为( )
长度的取值范围为( )
A.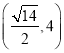 B.
B.![]() C.
C.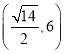 D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com