
(本小题12分)已知f(x)=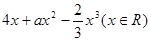 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=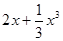 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(1) A={a|-1≤a≤1} (2) {m|m≥2,或m≤-2}
【解析】
试题分析:解:(Ⅰ)f'(x)=4+2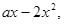 ∵f(x)在[-1,1]上是增函数,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设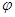 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
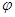 (1)=1-a-2≤0,
(1)=1-a-2≤0,
① 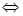
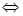 -1≤a≤1,
-1≤a≤1,
 (-1)=1+a-2≤0.
(-1)=1+a-2≤0.
∵对x∈[-1,1],只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
方法二:

(Ⅱ)由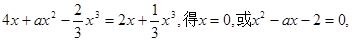
∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,
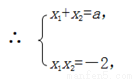
从而|x1-x2|=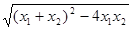 =
=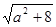 .
.
∵-1≤a≤1,∴|x1-x2|=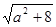 ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
②g(-1)=m2-m-2≥0,
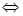 g(1)=m2+m-2≥0,
g(1)=m2+m-2≥0,
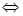 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,

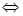 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
考点:函数单调性和函数与方程
点评:解决该试题的关键是能利用导数的符号判定函数单调性,同时能结合方程的思想来求解参数的范围,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(本小题12分)已知![]() ,
,![]() ,直线
,直线![]() 与函数
与函数![]() 、
、![]() 的k*s#5^u图象都相切,且与函数
的k*s#5^u图象都相切,且与函数![]() 的k*s#5^u图象的k*s#5^u切点的k*s#5^u横坐标为
的k*s#5^u图象的k*s#5^u切点的k*s#5^u横坐标为![]() .
.
(Ⅰ)求直线![]() 的k*s#5^u方程及
的k*s#5^u方程及![]() 的k*s#5^u值;
的k*s#5^u值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的k*s#5^u导函数),求函数
的k*s#5^u导函数),求函数![]() 的k*s#5^u最大值;
的k*s#5^u最大值;
(Ⅲ)当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011年四川省泸县二中高2013届春期重点班第一学月考试数学试题 题型:解答题
(本小题12分)已知等比数列 中,
中, 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设等差数列 中,
中, ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2011云南省潞西市高二上学期期末考试数学试卷 题型:解答题
(本小题12分)
已知顶点在原点,焦点在 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学文卷 题型:解答题
(本小题12分)
已知圆C: ;
;
(1)若直线 过
过 且与圆C相切,求直线
且与圆C相切,求直线 的方程.
的方程.
(2)是否存在斜率为1直线 ,使直线
,使直线 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届山东省兖州市高二下学期期末考试数学(文) 题型:解答题
(本小题12分)已知函数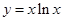
(1) 求这个函数的导数;
(2) 求这个函数的图像在点 处的切线方程。
处的切线方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com