
分析 (1)利用向量坐标运算,求出f(x)的表达式并化简,利用T=$\frac{2π}{ω}$求出T,再由函数单调性求出最大值;
(2)利用正弦型函数单调性,整体代入求出其单调递增区间;
(3)画出其一个周期函数图象.
解答 解:(1)由题意得:
f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}$cos4x+sin4x=2($\frac{\sqrt{3}}{2}$cos4x+$\frac{1}{2}$sin4x)=2sin(4x+$\frac{π}{3}$),
所以T=$\frac{2π}{ω}$=$\frac{π}{2}$,
f(x)max=2;
(2)因为当$-\frac{π}{2}+2kπ≤$4x+$\frac{π}{3}$$≤\frac{π}{2}+2kπ$(k∈Z)即$-\frac{5π}{24}+\frac{kπ}{2}≤x≤\frac{π}{24}+\frac{kπ}{2}$(k∈Z)时,y=f(x)单调增,
所以函数的递增区间为[$-\frac{5π}{24}+\frac{kπ}{2}$,$\frac{π}{24}+\frac{kπ}{2}$](k∈Z);
(3)函数图象如下:
点评 (1)本题主要考察向量坐标运算和辅助角公式,难度中档;(2)本题解题关键是利用整体代入求出x的取值范围,属于三角函数常见题型.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
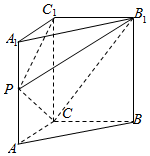 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
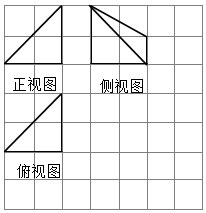 某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )
某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | 2 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
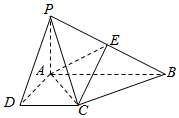 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
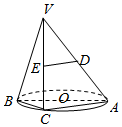 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$ | C. | $\root{4e}{e}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com