
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
![]()
根据以上数据,绘制了散点图.
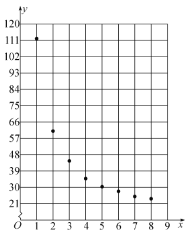
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .参考数据(其中
.参考数据(其中![]() ):
):

(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: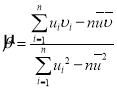 ,
,![]() ,相关系数
,相关系数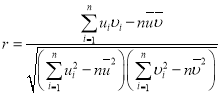 .
.
【答案】(1)![]() ;(2)当产量为10千件时,每件产品的非原料成本为21元;(3)见解析
;(2)当产量为10千件时,每件产品的非原料成本为21元;(3)见解析
【解析】
(1)令![]() ,则
,则![]() 可转化为
可转化为![]() ,分别求出
,分别求出![]() 的值,即可求解;
的值,即可求解;
(2)直接利用相关关系公式求得![]() 与
与![]() 的相关系数,可得
的相关系数,可得![]() ,得到用反比例函数模型拟合效果更好,取
,得到用反比例函数模型拟合效果更好,取![]() ,可得当
,可得当![]() 千件时,每件产品的分原料成本;
千件时,每件产品的分原料成本;
(3)分别求出产品单价为100元与产品单价为90元企业的利润,即可得到答案.
(1)令![]() ,则
,则![]() 可转化为
可转化为![]() ,
,
因为![]() ,所以
,所以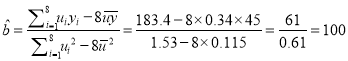 ,
,
则![]() ,所以
,所以![]() ,
,
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ;
;
(2)![]() 与
与![]() 的相关系数为:
的相关系数为:
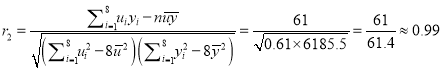 ,
,
因为![]() ,所以用反比例函数模型拟合效果更好,
,所以用反比例函数模型拟合效果更好,
当![]() 时,
时,![]() (元),
(元),
所以当产量为10千件时,每件产品的非原料成本为21元;
(3)(i)若产品单价为100元,记企业利润为![]() (千元),
(千元),
订单为9千件时,每件产品的成本为![]() 元,企业的利润为611(千元),
元,企业的利润为611(千元),
订单为10千件时,每件产品的成本为31元,企业的利润为690(千元),
企业利润![]() (千元)的分布列为
(千元)的分布列为
| 611 | 690 |
| 0.8 | 0.2 |
所以![]() (千元);
(千元);
(ii)若产品单价为90元,记企业利润为![]() (千元),
(千元),
订单为10千件时,每件产品的成本为31元,企业的利润为590(千元),
订单为11千件时,每件产品的成本为![]() 元,企业的利润为659(千元),
元,企业的利润为659(千元),
企业利润![]() (千元)的分布列为
(千元)的分布列为
| 590 | 659 |
| 0.3 | 0.7 |
所以![]() (千元),
(千元),
故企业要想获得更高利润,产品单价应选择90元.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
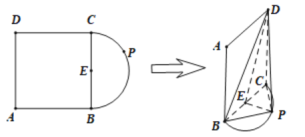
(1)证明:![]() 平面
平面![]() .
.
(2)三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”,其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,则该人第五天走的路程为( )
A. 6里B. 12里C. 24里D. 48里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共有编号分别为1,2,3,4,5的五个座位,在甲同学不坐2号座位,乙同学不坐5号座位的条件下,甲、乙两位同学的座位号相加是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,以
的左、右焦点,以![]() 为直径的圆与双曲线在第一象限和第三象限的交点分别为
为直径的圆与双曲线在第一象限和第三象限的交点分别为![]() ,
,![]() ,设四边形
,设四边形![]() 的周长为
的周长为![]() ,面积为
,面积为![]() ,且满足
,且满足![]() ,则该双曲线的离心率为______.
,则该双曲线的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店为了了解销售单价(单位:元)在![]() ]内的图书销售情况,从2018年上半年已经销售的图书中随机抽取100本,获得的所有样本数据按照
]内的图书销售情况,从2018年上半年已经销售的图书中随机抽取100本,获得的所有样本数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图,已知样本中销售单价在
分成6组,制成如图所示的频率分布直方图,已知样本中销售单价在![]() 内的图书数是销售单价在
内的图书数是销售单价在![]() 内的图书数的2倍.
内的图书数的2倍.
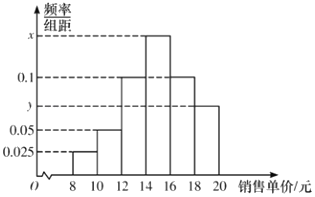
(1)求出![]() 与
与![]() ,再根据频率分布直方图估计这100本图书销售单价的平均数(同一组中的数据用该组区间的中点值作代表);
,再根据频率分布直方图估计这100本图书销售单价的平均数(同一组中的数据用该组区间的中点值作代表);
(2)用分层抽样的方法从销售单价在[8,20]内的图书中共抽取40本,求单价在6组样本数据中的图书销售的数量;
(3)从(2)中抽取且价格低于12元的书中任取2本,求这2本书价格都不低于10元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一.图中的窗花是由一张圆形纸片剪去一个正十字形剩下的部分,正十字形的顶点都在圆周上.已知正十字形的宽和长都分别为x,y(单位:dm)且x<y,若剪去的正十字形部分面积为4dm2.
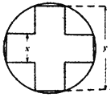
(1)求y关于x的函数解析式,并求其定义域;
(2)现为了节约纸张,需要所用圆形纸片面积最小.当x取何值时,所用到的圆形纸片面积最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com