
分析 根据函数零点的条件,求出相邻两个零点的间隔,进行求解即可.
解答 解:函数f(x)=2sin(2x-$\frac{π}{3}$)-1,
令f(x)=0,即2sin(2x-$\frac{π}{3}$)-1,
sin(2x-$\frac{π}{3}$)=$\frac{1}{2}$,
解得:x=$\frac{π}{4}+kπ$或x=$\frac{7π}{12}+kπ$,(k∈Z).
故相邻的零点之间的间隔依次为$\frac{π}{3}$,$\frac{2π}{3}$.
y=f(x)在[a,b]上至少含有10个零点,等价于b-a的最小值为4×$\frac{2π}{3}$+5×$\frac{π}{3}$=$\frac{13π}{3}$.
故答案为:$\frac{13π}{3}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数的对称性和函数零点的关系是解决本题的关键


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| B. | “x=1”是“x2-3x+2=0”的充分必要条件. | |
| C. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”是真命题 | |
| D. | 若¬(p∧q)为真命题,则p、q至少有一个为假命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x+\frac{1}{x}$ | B. | $f(x)=\frac{1}{x^2}$ | ||
| C. | $f(x)=\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$ | D. | $f(x)=\left\{\begin{array}{l}\frac{1}{2}{x^2}+1,x>0\\-\frac{1}{2}{x^2}-1,x<0\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
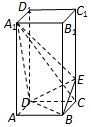 如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:
如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com