Question

【题目】设等差数列{an}的前n项和为Sn ， 且S4=4S2 ， a2n=2an+1．
（Ⅰ）求数列{an}的通项公式
（Ⅱ）设数列{bn}的前n项和为Tn ， 且 （λ为常数）．令cn=b2n ， （n∈N*），求数列{cn}的前n项和Rn ．

Answer 1

【答案】解：（Ⅰ）设等差数列{an}的首项为a1，公差为d．

由S4=4S2，a2n=2an+1．得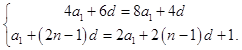

解得 a1=1，d=2．

因此 an=2n﹣1，n∈N*．

（II）由（I）可得 = ．

当n≥2时，bn=Tn﹣Tn﹣1= = ．

故 = ，n∈N*．

∴Rn=0+ …= ，

= + +…+ ，

两式相减得 = = ﹣ ，

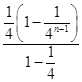∴Rn= ，

∴Rn= ．

∴数列{cn}的前n项和

【解析】（Ⅰ）设等差数列{an}的首项为a1，公差为d．由于S4=4S2，a2n=2an+1．利用等差数列的通项公式和前n项和公式可得

解出即可．（II））由（I）可得Tn．当n≥2时，bn=Tn﹣Tn﹣1．可得cn=b2n，n∈N*．再利用“错位相减法”即可得出Rn．

【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系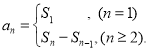，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．