
【题目】已知函数 ![]() 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式 ![]() 的解集为B,集合
的解集为B,集合 ![]() ,集合D={x|m+1≤x<2m﹣1}(m>0)
,集合D={x|m+1≤x<2m﹣1}(m>0)
(1)若A∪B=B,求实数a的取值范围;
(2)若DC,求实数m的取值范围.
【答案】
(1)解:因为f(x)在[ ![]() ,4]上,单调递增,
,4]上,单调递增,
∵f( ![]() )=
)= ![]() =﹣2,f(4)=log44=1,
=﹣2,f(4)=log44=1,
所以,A=[﹣2 1].
又由关于x的不等式 ![]() 可得 (2)﹣3x﹣a>2x,﹣3x﹣a>x x<﹣
可得 (2)﹣3x﹣a>2x,﹣3x﹣a>x x<﹣ ![]() ,
,
所以,B=(﹣∞,﹣ ![]() ).
).
又A∪B=B,∴AB.
所以,﹣ ![]() >1,a<﹣4,即实数a的取值范围为(﹣∞,﹣4)
>1,a<﹣4,即实数a的取值范围为(﹣∞,﹣4)
(2)解:因为 ![]() ,所以有
,所以有 ![]() ,所以﹣1<x≤5,所以,C=(﹣1,5],
,所以﹣1<x≤5,所以,C=(﹣1,5],
对于集合D={x|m+1≤x<2m﹣1}(m>0),若DC,有:
①当 m+1≥2m﹣1时,即 0<m≤2时,D=,满足 DC.
②当 m+1<2m﹣1 时,即 m>2时,D≠,所以有: ![]() ,解得﹣2<m≤3,又 m>2,2<m≤3.
,解得﹣2<m≤3,又 m>2,2<m≤3.
综上:由①②可得:实m的取值范围为(0,3]
【解析】(1)利用对数函数的单调性求对数函数的值域A,解指数不等式求出B,再根据AB可得﹣ ![]() >1,由此求得实数a的取值范围.(2)解分式不等式
>1,由此求得实数a的取值范围.(2)解分式不等式 ![]() 求得C,对于集合D={x|m+1≤x<2m﹣1}(m>0),由DC,分D=和 D≠两种情况,分别求出实m的取值范围,再取并集,即得所求.
求得C,对于集合D={x|m+1≤x<2m﹣1}(m>0),由DC,分D=和 D≠两种情况,分别求出实m的取值范围,再取并集,即得所求.


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为I的函数y=f(x),如果存在区间[m,n]I,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax﹣2a)+loga(ax﹣3a)(其中a>0且a≠1),求g(x)的定义域并判断其单调性;
(2)试判断(1)中的g(x)是否存在“好区间”,并说明理由;
(3)已知函数P(x)= ![]() (t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 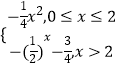 ,若关于x的方程[f(x)]2+af(x)+
,若关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
=0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量t(条)是售价x(元)(x∈Z+)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润﹣总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 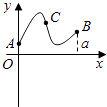
A.
B.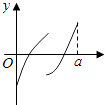
C.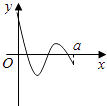
D.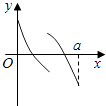
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
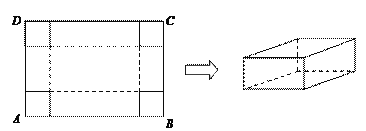
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/mm.
(1)求该游客离景点A的距离y(m)关于出发后的时间x(mm)的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点A的距离不小于1000m的总时长. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com