
【题目】为了发展电信事业方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费y(元)的关系分别如图①、②所示.

(1)分别求出通话费y1,y2与通话时间x之间的函数关系式;
(2)请帮助用户计算,在一个月内使用哪种卡便宜?
【答案】(1)y1=![]() x+29,y2=
x+29,y2=![]() x;(2)见解析.
x;(2)见解析.
【解析】
(1)由图可知,![]() 与通话时间
与通话时间![]() 成一次函数,
成一次函数,![]() 与通话时间
与通话时间![]() 成正比例函数,设出函数解析式,代入点的坐标得答案;
成正比例函数,设出函数解析式,代入点的坐标得答案;
(2)当两种卡的收费相等时,可求出![]() 值,当通话时间小于此值,便民卡便宜,当通话时间大于此值,如意卡便宜.
值,当通话时间小于此值,便民卡便宜,当通话时间大于此值,如意卡便宜.
(1)由图象可设y1=k1x+29,y2=k2x,把点B(30,35),C(30,15)分别代入y1,y2得k1=![]() ,k2=
,k2=![]() .
.
∴y1=![]() x+29,y2=
x+29,y2=![]() x.
x.
(2)令y1=y2,即![]() x+29=
x+29=![]() x,则x=96
x,则x=96![]() .
.
当x=96![]() 时,y1=y2,两种卡收费一致;
时,y1=y2,两种卡收费一致;
当x<96![]() 时,y1>y2,即使用“便民卡”便宜;
时,y1>y2,即使用“便民卡”便宜;
当x>96![]() 时,y1<y2,即使用“如意卡”便宜.
时,y1<y2,即使用“如意卡”便宜.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】某技校开展技能大赛,甲、乙两班各选取5名学生加工某种零件,在4个小时内每名学生加工的合格零件数的统计数据的茎叶图如图所示,已知甲班学生在4个小时内加工的合格零件数的平均数为21,乙班学生在4个小时内加工的合格零件数的平均数不低于甲班的平均数.
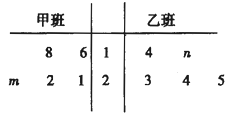
(1)求![]() 的值;
的值;
(2)分别求出甲、乙两班学生在4个小时内加工的合格零件数的方差![]() 和
和![]() ,并由此比较两班学生的加工水平的稳定性.
,并由此比较两班学生的加工水平的稳定性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 在第一线象限的交点为
在第一线象限的交点为![]() .
.

(1)求曲线![]() 、
、![]() 的方程;
的方程;
(2)在抛物线![]() 上任取一点
上任取一点![]() ,在点
,在点![]() 处作抛物线
处作抛物线![]() 的切线
的切线![]() ,若椭圆
,若椭圆![]() 上存在两点关于直线
上存在两点关于直线![]() 对称,求点
对称,求点![]() 的纵坐标的取值范围.
的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法正确的有( )
①函数的定义域和值域确定后,函数的对应关系也就确定了;
②f(x)=![]() 是函数;
是函数;
③函数y=2x(x∈N)的图象是一条直线;
④f(x)=![]() 与
与![]() 是同一函数.
是同一函数.
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数
,且存在实常数![]() ,使得对于定义域内任意
,使得对于定义域内任意![]() ,都有
,都有![]() 成立,则称此函数
成立,则称此函数![]() 具有“性质
具有“性质![]() ”.
”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有
性质”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 既具有“
既具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数
有2017个公共点,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com