
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1. 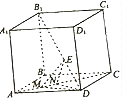
⑴当N为对角线AC的中点且DE= ![]() 时,则三棱锥E﹣DMN的体积是;
时,则三棱锥E﹣DMN的体积是;
⑵当三棱锥E﹣DMN的体积为 ![]() 时,则DE= .
时,则DE= .
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:
T(分钟) | 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求T的分布列与数学期望ET;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(b>a>0)的右焦点为F,O为坐标原点,若存在直线l过点F交双曲线C的右支于A,B两点,使
=1(b>a>0)的右焦点为F,O为坐标原点,若存在直线l过点F交双曲线C的右支于A,B两点,使 ![]()
![]() =0,则双曲线离心率的取值范围是 .
=0,则双曲线离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=eax+λlnx,其中a<0,0<λ< ![]() ,e是自然对数的底数
,e是自然对数的底数
(1)求证:函数f(x)有两个极值点;
(2)若﹣e≤a<0,求证:函数f(x)有唯一零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)ex , a∈R. (Ⅰ)当a=1时,试求f(x)的单调增区间;
(Ⅱ)试求f(x)在[1,2]上的最大值;
(Ⅲ)当a=1时,求证:对于x∈[﹣5,+∞), ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=4,BC=2,D,E分别为边AC,AB的中点,点F,G分别为线段CD,BE的中点.将△ADE沿DE折起到△A1DE的位置,使∠A1DC=60°.点Q为线段A1B上的一点,如图2. 
(Ⅰ)求证:A1F⊥BE;
(Ⅱ)线段A1B上是否存在点Q使得FQ∥平面A1DE?若存在,求出A1Q的长,若不存在,请说明理由;
(Ⅲ)当 ![]() 时,求直线GQ与平面A1DE所成角的大小.
时,求直线GQ与平面A1DE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|2x+2|﹣5(a∈R). (Ⅰ)试比较f(﹣1)与f(a)的大小;
(Ⅱ)当a≥﹣1时,若函数f(x)的图象和x轴围成一个三角形,则实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是 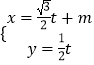 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com