
【题目】2022年第24届冬奥会将在中国北京和张家口举行,为了宣传冬奥会,某大学从全校学生中随机抽取了120名学生,对是否收看第23届平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表数据,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(2)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动,若从这8人中随机选取2人到较广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率.
附: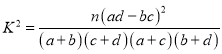 ,其中
,其中![]() .
.
P( | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
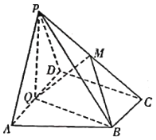
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 面
面![]() ;
;
(2)若二面角![]() 为
为![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线方程.
(1)经过点A(-1,-3),且斜率等于直线3x+8y-1=0斜率的2倍;
(2)过点M(0,4),且与两坐标轴围成三角形的周长为12.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 、
、![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的折线图是某超市2018年一月份至五月份的营业额与成本数据,根据该折线图,下列说法正确的是( )
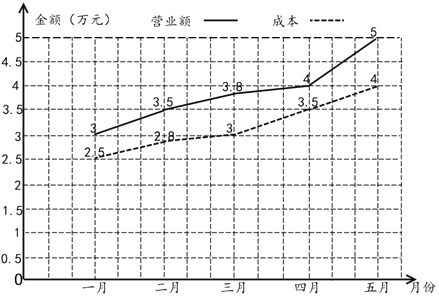
A.该超市2018年的前五个月中三月份的利润最高
B.该超市2018年的前五个月的利润一直呈增长趋势
C.该超市2018年的前五个月的利润的中位数为0.8万元
D.该超市2018年前五个月的总利润为3.5万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
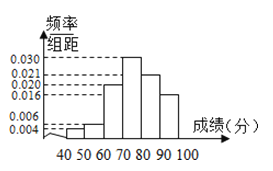
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车,调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值及续驶里程在
的值及续驶里程在![]() 的车辆数;
的车辆数;
(2)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com