
分析 设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,由点A(0,0),B(2,0),C(4,2),列出方程组,能求出△ABC的外心的纵坐标.
解答 解:设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,
∵点A(0,0),B(2,0),C(4,2),
∴$\left\{\begin{array}{l}{F=0}\\{4+2D+F=0}\\{20+4D+2E+F=0}\end{array}\right.$,
解得D=-2,E=-6,F=0,
∴△ABC外接圆方程为x2+y2-2x-6y=0.
∴△ABC外接圆的圆心为(1,3),
∴△ABC的外心的纵坐标是3.
故答案为:3.
点评 本题考查三角形外心纵坐标的求法,是基础题,解题时要认真审题,注意待定系数法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | -$\frac{3}{7}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, ,
,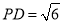 ,
, 为
为 与
与 的交点,
的交点, 为棱
为棱 上一点.
上一点.

(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)若 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为 ,
,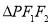 是以
是以 为底边的等腰三角形,若
为底边的等腰三角形,若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com