
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,左右两顶点
,左右两顶点![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,满足直线
上任意一点,满足直线![]() 的斜率之积为
的斜率之积为![]() ,且
,且![]() 的最大值为4.
的最大值为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与过点
与过点![]() 且与
且与![]() 轴垂直的直线交于点
轴垂直的直线交于点![]() ,过点
,过点![]() 作
作![]() ,垂足分别为
,垂足分别为![]() 两点,求证:
两点,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于-1的直线与椭圆
且斜率等于-1的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
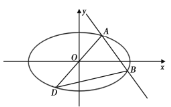
(1)证明:直线![]() 的斜率为定值;
的斜率为定值;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

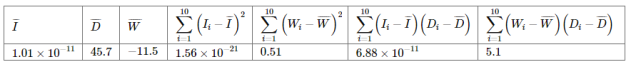
表中![]() ,
,![]()
(1)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程
的回归方程![]() ;
;
(2)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪声污染的干扰,并说明理由.
点是否受到噪声污染的干扰,并说明理由.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: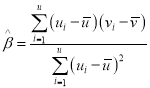 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,左右两顶点
,左右两顶点![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,满足直线
上任意一点,满足直线![]() 的斜率之积为
的斜率之积为![]() ,且
,且![]() 的最大值为4.
的最大值为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过
,过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 相交与
相交与![]() 两点,连接点
两点,连接点![]() 并延长,交轨迹
并延长,交轨迹![]() 于一点
于一点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD为菱形,
的底面ABCD为菱形,![]() ,侧面PAD与底面ABCD所成的角为
,侧面PAD与底面ABCD所成的角为![]() ,
,![]() 是等边三角形,点P到平面ABCD距离为
是等边三角形,点P到平面ABCD距离为![]() .
.
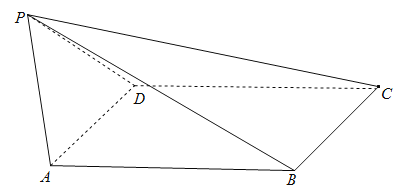
(1)证明:![]() ;
;
(2)求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中, ![]() ,动点
,动点![]() 满足:以
满足:以![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 两点,当
两点,当![]() 与
与![]() 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com