
| | 第1批次 | 第2批次 | 第3批次 |
| 第一轮检测 |  |  |  |
| 第二轮检测 |  |  |  |
 ,求
,求 的分布列及数学期望
的分布列及数学期望
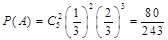
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
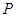 | 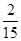 | 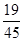 | 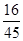 | 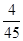 |
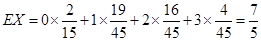
 ,不合格的概率为
,不合格的概率为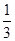 ,则
,则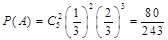
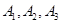
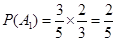 ,
,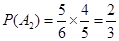 ,
,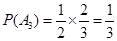
 的可能取值为0,1,2,3
的可能取值为0,1,2,3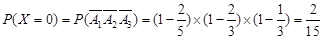
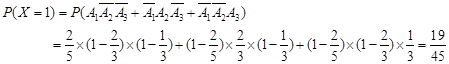
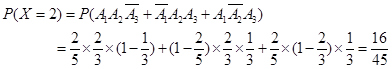
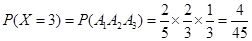
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
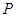 | 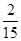 | 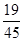 | 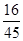 | 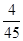 |
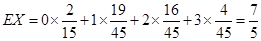


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源:不详 题型:解答题
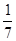 ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。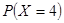 ;
;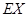 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 层下电梯的概率
层下电梯的概率 ;
; 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分, 同学成绩为95分,求
同学成绩为95分,求 、
、 两同学恰好被安排在“二帮一”中同一小组的概率.
两同学恰好被安排在“二帮一”中同一小组的概率.| 分 组 | 频 数 | 频 率 |
| [40, 50 ) | 2 | 0.04 |
| [ 50, 60 ) | 3 | 0.06 |
| [ 60, 70 ) | 14 | 0.28 |
| [ 70, 80 ) | 15 | 0.30 |
| [ 80, 90 ) | | |
| [ 90, 100 ] | 4 | 0.08 |
| 合 计 | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:| 班级 | 一班 | 二班 | 三班 | 四班 |
| 人数 | 2人 | 3人 | 4人 | 1人 |
 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为 ;选择
;选择 音乐的概率都为
音乐的概率都为 ;选择
;选择 读书的概率都为
读书的概率都为 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com