
分析 (1)求出函数的定义域,导函数,通过导函数大于0求解函数的单调增区间.
(2)化简F(x)=f(x)+g(x),构造函数,利用导函数通过m 的范围,判断函数的单调性求解函数的最值.推出m的最小值即可.
(3)m=-1时,F(x)=lnx+$\frac{1}{2}$x2+x,x>0,由F(x1)=-F(x2),推出lnx1+$\frac{1}{2}$${{x}_{1}}^{2}$+x1+lnx2+$\frac{1}{2}$${{x}_{2}}^{2}$+x2=0,令t=x1•x2>0,由φ(t)=t-lnt,求出φ′(t)=$\frac{t-1}{t}$,利用函数的单调性求解函数的最值,然后推出x1+x2≥$\sqrt{3}$-1成立..
解答 解:(1)f(x)的定义域为:{x|x>0},f′(x)=$\frac{1}{x}$-x=$\frac{1-{x}^{2}}{x}$,(x>0),
由f′(x)>0,得:0<x<1,所以f(x)的单调递增区间为(0,1).…(4分)
(2)F(x)=f(x)+g(x)=lnx-$\frac{1}{2}$mx2+x,x>0,
令G(x)=F(x)-(mx-1)=lnx-$\frac{1}{2}$mx2+(1-m)x+1,
则不等式F(x)≤mx-1恒成立,即G(x)≤0恒成立.
G′(x)=$\frac{1}{x}$-mx+(1-m)=$\frac{-m{x}^{2}-(1-m)x+1}{x}$,
①当m≤0时,因为x>0,所以G′(x)>0所以G(x)在(0,+∞)上是单调递增函数,
又因为G(1)=ln1-$\frac{1}{2}$m×12+(1-m)+1=-$\frac{3}{2}$m+2>0,所以关于x的不等式G(x)≤0不能恒成立,
②当m>0时,G′(x)=-$\frac{m(x-\frac{1}{m})(x-1)}{x}$,令G′(x)=0,因为x>0,得x=$\frac{1}{m}$,
所以当x∈(0,$\frac{1}{m}$)时,G′(x)>0;当x∈($\frac{1}{m}$,+∞)时,G′(x)<0,
因此函数G(x)在x∈(0,$\frac{1}{m}$)是增函数,在x∈($\frac{1}{m}$,+∞)是减函数,
故函数G(x)的最大值为:G($\frac{1}{m}$)=ln$\frac{1}{m}$-$\frac{1}{2}$m×$(\frac{1}{m})^{2}$+(1-m)×$\frac{1}{m}$+1=$\frac{1}{2m}$-lnm,
令h(m)=$\frac{1}{2m}$-lnm,因为h(m)在m∈(0,+∞)上是减函数,
又因为h(1)=$\frac{1}{2}$>0,h(2)=$\frac{1}{4}$-ln2<0,所以当m≥2时,h(m)<0,
所以整数m的最小值为2. …(10分)
(3)m=-1时,F(x)=lnx+$\frac{1}{2}$x2+x,x>0,
由F(x1)=-F(x2),得F(x1)+F(x2)=0,即lnx1+$\frac{1}{2}$${{x}_{1}}^{2}$+x1+lnx2+$\frac{1}{2}$${{x}_{2}}^{2}$+x2=0,
整理得:$\frac{1}{2}$$({x}_{1}+{x}_{2})^{2}$+(x1+x2)=x1 x2-ln(x1 x2),
令t=x1•x2>0,则由φ(t)=t-lnt,得:φ′(t)=$\frac{t-1}{t}$,
可知φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上
单调递增,所以φ(t)≥φ(1)=1,
所以:$\frac{1}{2}$$({x}_{1}+{x}_{2})^{2}$+(x1+x2)≥1,解得:x1+x2≤-$\sqrt{3}$-1,或x1+x2≥$\sqrt{3}$-1,
因为x1,x2为正整数,所以:x1+x2≥$\sqrt{3}$-1成立. …(15分)
点评 本题考查函数的导数的综合应用,函数的单调性以及极值以及函数的最值,构造法的应用,考查转化思想以及计算能力.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{3}$ | B. | $±\sqrt{13}$ | C. | ±4 | D. | $±2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?x∈R,\root{3}{x}+1>0$ | |
| B. | 小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件 | |
| C. | p∨q为真命题,则命题p与q均为真命题 | |
| D. | 命题“$?{x_0}∈R,{x_0}^2-{x_0}>0$的命题的否定是“?x∈R,x2-x≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
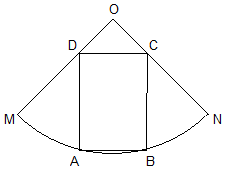 如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com