
【题目】设![]() ,
,![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,点
,点![]() (
(![]() )均在函数
)均在函数![]() 的图像上.
的图像上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求满足
项和,求满足![]() (
(![]() )的最大正整数
)的最大正整数![]() .
.
【答案】(1)an=6n-5 (![]() ) (2)8
) (2)8
【解析】
(1)根据f(x)=3x2﹣2x,由(n,Sn)在y=3x2﹣2x上,知Sn=3n2﹣2n.由此能求出数列{an}的通项公式.
(2)由![]() ,知Tn
,知Tn![]() (1-
(1-![]() ),根据
),根据![]() (
(![]() )对
)对![]() 恒成立,当且仅当
恒成立,当且仅当![]() ,由此能求出所有n∈N*都成立的m的范围.
,由此能求出所有n∈N*都成立的m的范围.
(1)因为![]() =3x2-2x.
=3x2-2x.
又因为点![]() 均在函数
均在函数![]() 的图像上,所以
的图像上,所以![]() =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-![]() =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=1,所以,an=6n-5 (![]() ).
).
(2)由(1)得知![]() =
=![]() ,
,
故Tn=![]() =
=![]()
![]()
=![]() (1-
(1-![]() ),且Tn随着n的增大而增大
),且Tn随着n的增大而增大
因此,要使![]() (1-
(1-![]() )
)![]() (
(![]() )对
)对![]() 恒成立,当且仅当n=1时T1=
恒成立,当且仅当n=1时T1=![]() ,
,
即m<9,所以满足要求的最大正整数m为8.


科目:高中数学 来源: 题型:
【题目】已知正三棱锥![]() ,一个正三棱柱的一个底面的三个顶点在正三棱锥的三条侧棱上,另一底面在正三棱锥的底面上,若正三棱锥的高为15,底面边长为12,内接正三棱柱的侧面积为120.
,一个正三棱柱的一个底面的三个顶点在正三棱锥的三条侧棱上,另一底面在正三棱锥的底面上,若正三棱锥的高为15,底面边长为12,内接正三棱柱的侧面积为120.
(1)求三棱柱的高;
(2)求棱柱的上底面截棱锥所得的小棱锥与原棱锥的侧面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路汽车的车流量![]() (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度![]() 之间的函数关系式为:
之间的函数关系式为:![]() .
.
(1)若要求在该段时间内车流量超过2千辆![]() ,则汽车在平均速度应在什么范围内?
,则汽车在平均速度应在什么范围内?
(2)在该时段内,若规定汽车平均速度不得超过![]() ,当汽车的平均速度
,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连结
上,连结![]() .
.
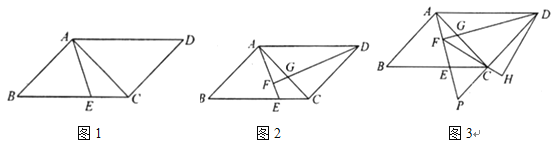
(1)若![]() ,求
,求![]() 的周长;
的周长;
(2)点![]() 是
是![]() 上一点,连结
上一点,连结![]() 交
交![]() 于点
于点![]() .
.
①如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
②如图3,连结![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 延长
延长![]() 交
交![]() 延长线于点
延长线于点![]() ,请直接写出线段
,请直接写出线段![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com