【题目】在高山滑雪运动的曲道赛项目中，运动员从高处（起点）向下滑，在滑行中运动员要穿过多个高约0.75米，宽4至6米的旗门，规定：运动员不经过任何一个旗门，都会被判一次“失格”，滑行时间会被增加，而所用时间越少，则排名越高.已知在参加比赛的运动员中，有五位运动员在滑行过程中都有三次“失格”，其中
（1）甲在滑行过程中依次没有经过
，
，
三个旗门；
（2）乙在滑行过程中依次没有经过
，
，
三个旗门；
（3）丙在滑行过程中依次没有经过
，，三个旗门；
（4）丁在滑行过程中依次没有经过，，
三个旗门；
（5）戊在滑行过程中依次没有经过，，三个旗门.
根据以上信息，，，，，，，，这8个旗门从上至下的排列顺序共有（ ）种可能.
A.6B.7C.8D.12
科目：高中数学 来源： 题型：
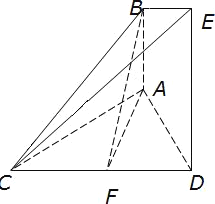
【题目】如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．
（1）求证：AF∥平面BCE；
（2）求证：平面BCE⊥平面CDE；
（3）求直线BF和平面BCE所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角梯形
中，
，
，
，直角梯形
可以通过直角梯形以直线
为轴旋转得到，且平面
平面.
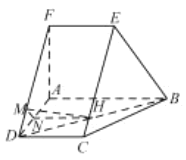
（1）求证：
；
（2）设
、
分别为
、
的中点，
为线段
上的点（不与点
重合）.
（i）若平面
平面，求
的长；
（ii）线段上是否存在，使得直线
平面
，若存在求的长，若不存在说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中函数
，
.
（1）求函数
在点
处的切线方程；
（2）当
时，求函数
在
上的最大值；
（3）当
时，对于给定的正整数
，问：函数
是否有零点？请说明理由.（参考数据
，
，
，
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，将数字1,2,3，…， 
（
）全部填入一个2行
列的表格中，每格填一个数字，第一行填入的数字依次为
， 
，…， 
，第二行填入的数字依次为
， 
，…， 
．记
．
（Ⅰ）当
时，若
， 
， 
，写出
的所有可能的取值；
（Ⅱ）给定正整数
．试给出
， 
，…， 
的一组取值，使得无论
， 
，…， 
填写的顺序如何， 
都只有一个取值，并求出此时
的值；
（Ⅲ）求证：对于给定的
以及满足条件的所有填法， 
的所有取值的奇偶性相同.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若无穷数列
满足：
是正实数，当
时，
，则称是“
—数列”.
（1）若是“—数列”且
，写出
的所有可能值；
（2）设是“—数列”，证明：是等差数列当且仅当单调递减；是等比数列当且仅当单调递增；
（3）若是“—数列”且是周期数列（即存在正整数
，使得对任意正整数
，都有
），求集合
的元素个数的所有可能值的个数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学2018年的高考考生人数是2015年高考考生人数的
倍，为了更好地对比该校考生的升学情况，统计了该校2015年和2018年的高考情况，得到如图柱状图：
则下列结论正确的是
A. 与2015年相比，2018年一本达线人数减少
B. 与2015年相比，2018年二本达线人数增加了
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比，2018年不上线的人数有所增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合
的元素均为实数，若对任意
，存在
，
，使得
且
，则称元素个数最少的
和
为的“孪生集”；称的“孪生集”的“孪生集”为的“2级孪生集”；称的“2级孪生集”的“孪生集”为的“3级孪生集”，依此类推……
（1）设
，直接写出集合的“孪生集”；
（2）设元素个数为
的集合的“孪生集”分别为和，若使集合
中元素个数最少且所有元素之和为2，证明：中所有元素之和为
；
（3）若
，请直接写出的“级孪生集”的个数，及所有“级孪生集”的并集
的元素个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
