
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,以原点为圆心,椭圆的半焦距为半径的圆与直线
,以原点为圆心,椭圆的半焦距为半径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积
的面积![]() 满足:
满足: ![]() ,求直线
,求直线![]() 的斜率.
的斜率.
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为![]() ,其范围为
,其范围为![]() ,分为五个级别,
,分为五个级别, ![]() 畅通;
畅通; ![]() 基本畅通;
基本畅通; ![]() 轻度拥堵;
轻度拥堵; ![]() 中度拥堵;
中度拥堵; ![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.

(1)这50个路段为中度拥堵的有多少个?
(2)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟,中度拥堵为42分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数![]() (单位:公里)分为3类,即
(单位:公里)分为3类,即![]() ,
, ![]() ,
, ![]() .对这140辆车的行驶总里程进行统计,结果如下表:
.对这140辆车的行驶总里程进行统计,结果如下表:

(1)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率; (2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车. (ⅰ)求
辆车. (ⅰ)求![]() 的值; (ⅱ)如果从这
的值; (ⅱ)如果从这![]() 辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求证:f(x)+f(1﹣x)= ![]() ;
;
(2)设数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1),求an;
)+f(1),求an;
(3)设数列{an}的前项n和为Sn , 若Sn≥λan(n∈N*)恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(2x+
sin(2x+ ![]() ),其中x∈R,下列结论中正确的是( )
),其中x∈R,下列结论中正确的是( )
A.f(x)是最小正周期为π的偶函数
B.f(x)的一条对称轴是 ![]()
C.f(x)的最大值为2
D.将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位得到函数f(x)的图象
个单位得到函数f(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
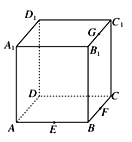
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l2分)
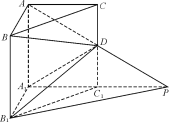
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 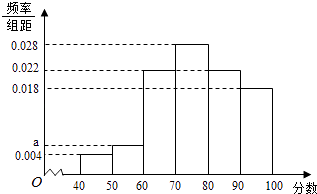
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:
(1)2sinBcosC﹣sin(B﹣C)的值;
(2)若a=2,求△ABC周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com