
(本题满分12分)在△ABC中,若 。
。
(1)求 的值;
的值;
(2)若 ,求
,求 和
和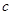 。
。
科目:高中数学 来源: 题型:解答题
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com