
【题目】盒子中有5个大小形状完全相同的小球,其中黑色小球有3个,标号分别为1,2,3,白色小球有2个,标号分别为1,2.
(1)若从盒中任取两个小球,求取出的小球颜色相同且标号之和小于或等于4的概率;
(2)若盒子里再放入一个标号为4的红色小球,从中任取两个小球,求取出的两个小球颜色不同且标号之和大于3的概率.
【答案】
(1)解:设黑色小球为A1,A2,A3,白色小球为B1,B2,
从盒子中任取两个小球,其一切可能的结果组成的基本事件有:
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10个,
根据题意,这些基本事件是等可能的,
事件“取出的小球颜色相同且标号之和小于或等于4”包含的基本事件有:
{A1,A2},{A1,A3},{B1,B2},共3个,
∴取出的小球颜色相同且标号之和小于或等于4的概率p1= ![]() .
.
(2)解:设红色小球为C4,从盒子中任取两个小球,其一切可能的结果组成的基本事件有:
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},
{A3,B2},{B1,B2},{A1,C4},{A2,C4},{A3,C4},{B1,C4},{B2,C4},共15个,
根据题意这些基本事件是等可能的,
事件“取出的两个小球颜色不同且标号之和大于3”所包含的基本事件有:
{A1,C4},{A2,B2},{A2,C4},{A3,B1},{A3,B2},{A3,C4},{B1,C4},{B2,C4},共8个,
∴取出的两个小球颜色不同且标号之和大于3的概率p2= ![]() .
.
【解析】(1)设黑色小球为A1 , A2 , A3 , 白色小球为B1 , B2 , 利用列举法能求出取出的小球颜色相同且标号之和小于或等于4的概率.(2)设红色小球为C4 , 利用列举法能求出取出的两个小球颜色不同且标号之和大于3的概率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观测点A,B(假设A,B,C,D在同一水平面上),且AB=80米,当航模在C 处时,测得∠ABC=
105°和∠BAC=30°,经过20秒后,航模直线航行到D 处,测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD= ![]() .用向量法解决下列问题:
.用向量法解决下列问题: 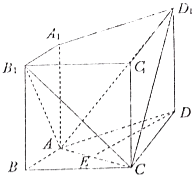
(1)若AC的中点为E,求A1C与DE所成的角;
(2)求二面角B1﹣AC﹣D1(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在直线x+y﹣2=0上.
(1)求圆M的方程.
(2)设P是直线3x+4y+8=0上的动点,PC、PD是圆M的两条切线,C、D为切点,求四边形PCMD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点 
(1)求证:AC⊥BC1;
(2)求异面直线AC1与CB1所成角的余弦值;
(3)求二面角D﹣CB1﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆 ![]() 和圆
和圆 ![]() ,
,
(1)若直线l1过点A(2,0),且与圆C1相切,求直线l1的方程;
(2)若直线l2过点B(4,0),且被圆C2截得的弦长为 ![]() ,求直线l2的方程.
,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过5吨时,每吨为2.6元,当用水超过5吨时,超过部分每吨4元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费34.7元,分别求甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m(sinx+cosx)﹣4sinxcosx,x∈[0, ![]() ],m∈R.
],m∈R.
(1)设t=sinx+cosx,x∈[0, ![]() ],将f(x)表示为关于t的函数关系式g(t),并求出t的取值范围;
],将f(x)表示为关于t的函数关系式g(t),并求出t的取值范围;
(2)若关于x的不等式f(x)≥0对所有的x∈[0, ![]() ]恒成立,求实数m的取值范围;
]恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)﹣2m+4=0在[0, ![]() ]上有实数根,求实数m的取值范围.
]上有实数根,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com