已知f(x)是偶函数.x≥0时.f(x)=-2x2+4x．画出f(x)在R上的函数图象．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

9．已知f（x）是偶函数，x≥0时，f（x）=-2x²+4x．画出f（x）在R上的函数图象．

分析利用偶函数的定义，若x＜0，则-x＞0，代入已知解析式且f（-x）=f（x），得所求解析式；根据函数解析式，画出函数f（x）的图象．

解答解：若x＜0，则-x＞0，
∵函数f（x）是定义在R上的偶函数，x≥0时，f（x）=-2x²+4x
∴f（x）=f（-x）=[-2（-x）²-+4（-x）]=-2x²-4x
函数f（x）的图象如图所示．

点评本题考查了偶函数的定义及其应用，利用函数的对称性求函数值及函数解析式，属于中档题．

练习册系列答案

四川名校初升高自主招生一本通系列答案

北教传媒实战中考系列答案

宏翔文化寒假一本通期末加寒假加预习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

19．已知ax³=by³=cz³，且$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=1，求证：（ax²+by²+cz²）${\;}^{\frac{1}{3}}$=a${\;}^{\frac{1}{3}}$+b${\;}^{\frac{1}{3}}$+c${\;}^{\frac{1}{3}}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．

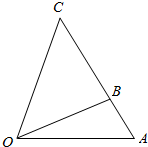在2014年亚洲移动通信博览会上，中国移动表示投资将超过2400亿元，根据规划，某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站，甲站建立在区域BOC内，乙站建立区域AOB内，分界线OB固定，且OB=（1+$\sqrt{3}$）km，边界线AC始终过点B，∠AOC=75°，∠AOB=30°，设OA=x（3≤x≤6）km，OC=ykm
（1）试将y表示成x的函数，并求出函数y的解析式
（2）当x取何值时，两个基站的占地面积S_△OAC最小？并求出最小面积．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．定义在R上的偶函数f（x）和奇函数g（x）满足f（x）+g（x）=2x，则g（2）=4．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．设f（x）=lg（$\frac{2}{1-x}$+a）是奇函数．
（1）求实数a的值；
（2）求函数的定义域；
（3）若x∈[$\frac{1}{2}$，$\frac{10}{11}$]，求f（x）的值域：

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．f（x）=$\left\{\begin{array}{l}{{e}^{x-1}，x＞1}\\{（1-2a）x-2，x≤1}\end{array}\right.$是R上的单调函数，则a的取值范围是[-1，$\frac{1}{2}$）．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．在直线3x-y+1=0上有一点A，它到点B（1，-1）和点C（2，0）等距离，则A点坐标为（0，1）．