
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.已知函数
的不动点.已知函数![]()
![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求
恒有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的两个不动点为
的两个不动点为![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
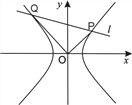
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x,f(a+2)=27,函数g(x)=λ·2ax-4x的定义域为[0,2].
(1)求a的值;
(2)若函数g(x)在[0,2]上单调递减,求λ的取值范围;
(3)若函数g(x)的最大值是![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:x2+2y2=4,
(1)求椭圆C的离心率
(2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,求直线AB与圆x2+y2=2的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 |
| ||
女性市民 |
| ||
总计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为支持申办
的前提下认为支持申办![]() 年足球世界杯与性别有关?请说明理由.
年足球世界杯与性别有关?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com