
【题目】如图一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为![]() ,设∠AOE=
,设∠AOE=![]() ,探照灯O照射在长方形ABCD内部区域的面积为S.
,探照灯O照射在长方形ABCD内部区域的面积为S.
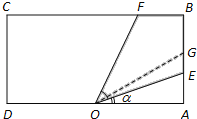
(1)当0≤![]()
![]() 时,写出S关于
时,写出S关于![]() 的函数表达式;
的函数表达式;
(2)若探照灯每9分钟旋转“一个来回”(OE自OA转到OC,再回到OA,称“一个来回”,忽略OE在OA及OC反向旋转时所用时间),且转动的角速度大小一定,设AB边上有一点G,且∠AOG![]() ,求点G在“一个来回”中,被照到的时间.
,求点G在“一个来回”中,被照到的时间.
【答案】(1),S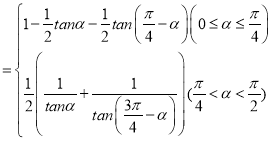 (2)2分钟
(2)2分钟
【解析】
(1) 根据AD=2,AB=1,0≤![]()
![]() ,确定点E,F的位置,分0≤
,确定点E,F的位置,分0≤![]()
![]() ,
,![]()
![]()
![]() ,两种情况,利用三角形面积公式求解.
,两种情况,利用三角形面积公式求解.
(2)先得到“一个来回”中,OE共转了2![]() ,其中点G被照到时,共转了2
,其中点G被照到时,共转了2![]() ,再利用角度关系求解.
,再利用角度关系求解.
如图所示:
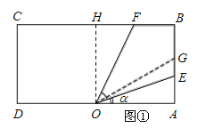
(1)过O作OH⊥BC,H为垂足.
①当0≤![]()
![]() 时,E在边AB上,F在线段BH上(如图①),
时,E在边AB上,F在线段BH上(如图①),
此时,AE=tan![]() ,FH=tan(
,FH=tan(![]()
![]() ),
),
∴S=S正方形OABH﹣S△OAE﹣S△OHF=1![]() tan
tan![]()
![]() tan(
tan(![]()
![]() ).
).
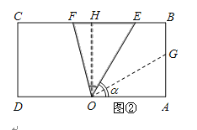
②当![]()
![]()
![]() 时,
时,
E在线段BH上,F在线段CH上(如图②),
此时,EH![]() ,FH
,FH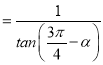 ,可得EF
,可得EF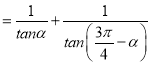 .
.
∴S=S△OEF![]() (
( ).
).
综上所述,S
(2)在“一个来回”中,OE共转了2![]() ,
,
其中点G被照到时,共转了2![]()
∴在“一个来回”中,点G被照到的时间为9![]() 2(分钟).
2(分钟).


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 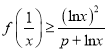 ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据切线过点
,再根据切线过点![]() ,解得
,解得![]() 导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为
导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为![]() ,分离得
,分离得![]() ,再利用导数求函数
,再利用导数求函数![]() 单调性,利用罗伯特法则求最大值,即得
单调性,利用罗伯特法则求最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,即
,即![]()
由题意得![]() ,解得
,解得![]()
所以![]()
从而![]()
因为当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在区间
在区间![]() 上是减函数,区间
上是减函数,区间![]() 上是增函数,
上是增函数,
从而![]() .
.
(2)由题意知,当![]() 时,
时, ![]() ,所以
,所以![]()
从而当![]() 时,
时, ![]() ,
,
由题意知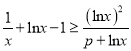 ,即
,即![]() ,其中
,其中![]()
设![]() ,其中
,其中![]()
设![]() ,即
,即![]() ,其中
,其中![]()
则![]() ,其中
,其中![]()
(1)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是增函数
是增函数
从而当![]() 时,
时, ![]() ,
,
所以![]() 是增函数,从而
是增函数,从而![]() .
.
故当![]() 时符合题意.
时符合题意.
(2)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是减函数
上是减函数
从而当![]() 时,
时, ![]()
所以![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]()
故当![]() 时不符合题意.
时不符合题意.
(3)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是减函数
是减函数
从而当![]() 时,
时, ![]()
所以![]() 是减函数,从而
是减函数,从而![]()
故当![]() 时不符合题意
时不符合题意
综上![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
22
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,点
,点![]() 是线段
是线段![]() 的中点。
的中点。
(1)求直线![]() 的方程;
的方程;
(2)是否存在与直线![]() 平行的直线
平行的直线![]() ,使得
,使得![]() 与与圆
与与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 不经过点
不经过点![]() ,且
,且![]() 的面积
的面积![]() 最大?若存在,求出
最大?若存在,求出![]() 的方程及对应的
的方程及对应的![]() 的面积S;若不存在,请说明理由。
的面积S;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数函数g(x)=1ogax(a>0,a≠1)和指数函数f(x)=ax(a>0,a≠1)互为反函数.已知函数f(x)=3x,其反函数为y=g(x).
(Ⅰ)若函数g(kx2+2x+1)的定义域为R,求实数k的取值范围;
(Ⅱ)若0<x1<x2且|g(x1)|=|g(x2)|,求4x1+x2的最小值;
(Ⅲ)定义在I上的函数F(x),如果满足:对任意x∈I,总存在常数M>0,都有-M≤F(x)≤M成立,则称函数F(x)是I上的有界函数,其中M为函数F(x)的上界.若函数h(x)=![]() ,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)当![]() 时,若方程
时,若方程![]() 在区间
在区间![]() 上有唯一解,求
上有唯一解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com