若 均为单位向量,且
均为单位向量,且 ,
,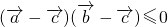 ,则
,则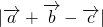 的最大值为________.
的最大值为________.
1
分析:由
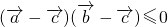
,以及

均为单位向量,且

,可得到
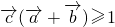
要求则
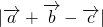
的最大值,只需将其平方化为数量积的运算即可求解.
解答:∵
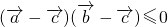
,即
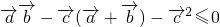
又

均为单位向量,且

,
所以
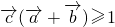
,-
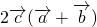
≤-2
故

=
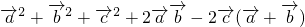
=3-
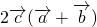
≤3-2=1
所以
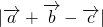
的最大值为:1
故答案为:1
点评:本题考查平面向量数量积的运算和模的计算问题,应特别注意有关模的问题一般采取平方法进行解决,属中档题.
练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年重庆市高三上学期半期考试理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2011-2012学年宁夏高三第六次月考理科数学试卷
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2011-2012年辽宁省庄河六高高二上学期开学初考试联考理科数学
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江西师大附中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省扬州市宝应中学高三数学自主训练试卷(21)(解析版)
题型:填空题
查看答案和解析>>

 均为单位向量,且
均为单位向量,且 ,
,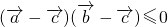 ,则
,则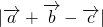 的最大值为________.
的最大值为________. 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案