
���� ��������������꣬����$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$���c2���ٽ�ϵ�$P��\frac{{2\sqrt{6}}}{3}��\frac{{\sqrt{3}}}{3}��$����Բ�ϼ������������a2��b2��ֵ�ô𰸣�
���������֪��0���ˣ�1����$��=\frac{{|\overrightarrow{QB}|}}{{|\overrightarrow{QA}|}}$����$\overrightarrow{QB}=��\overrightarrow{QA}$��Ȼ���ֱ��l��б�ʴ��ںͲ�������⣬��ֱ��l��б�ʴ���ʱ������ֱ�߷��̺���Բ���̣����ø���ϵ���Ĺ�ϵ��⣮
��� �⣺������F1��-c��0����F2��c��0��������$c=\sqrt{{a^2}-{b^2}}$��
����$\overrightarrow{P{F_1}}=��\frac{{2\sqrt{6}}}{3}+c��\frac{{\sqrt{3}}}{3}��$��$\overrightarrow{P{F_2}}=��\frac{{2\sqrt{6}}}{3}-c��\frac{{\sqrt{3}}}{3}��$��
����$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$����$��\frac{{2\sqrt{6}}}{3}+c����\frac{{2\sqrt{6}}}{3}-c��+{��\frac{{\sqrt{3}}}{3}��^2}=0$��
���c2=3��
�ֵ�P����ԲC�ϣ���$\frac{{{{��\frac{{2\sqrt{6}}}{3}��}^2}}}{a^2}+\frac{{{{��\frac{{\sqrt{3}}}{3}��}^2}}}{b^2}=1$����$\frac{8}{a^2}+\frac{1}{b^2}=3$��
��a2-b2=c2=3����b2=a2-3��
����������ʽ��������3a4-18a2+24=0�����a2=2���ᣩ����a2=4��
��b2=1��
���ǣ��������ԲC�ı�����Ϊ$\frac{x^2}{4}+{y^2}=1$��
���������֪��0���ˣ�1��
���ǣ���$��=\frac{{|\overrightarrow{QB}|}}{{|\overrightarrow{QA}|}}$����$\overrightarrow{QB}=��\overrightarrow{QA}$��
��1����ֱ��l��б�ʲ�����ʱ��
��ã�B��0��-1����A��0��1����
��$|\overrightarrow{QB}|=1��|\overrightarrow{QA}|=3$��
��ʱ$��=\frac{{|\overrightarrow{QB}|}}{{|\overrightarrow{QA}|}}=\frac{1}{3}$��
��2����ֱ��l��б�ʴ���ʱ����Ϊk����ֱ��l�ķ���Ϊy=kx-2����
���A��x1��y1����B��x2��y2�������ٴ���$\frac{x^2}{4}+{y^2}=1$��ȥy�ã���1+4k2��x2-16kx+12=0��
�ɡ�=162k2-4��12����1+4k2����0�����${k^2}��\frac{3}{4}$��
${x_1}+{x_2}=\frac{16k}{{1+4{k^2}}}$��${x_1}{x_2}=\frac{12}{{1+4{k^2}}}$����
��$\overrightarrow{QB}=��\overrightarrow{QA}$���ࣨx2��y2+2��=�ˣ�x1��y1+2����
����x2=��x1����
���۴���ڵ�$��1+�ˣ�{x_1}=\frac{16k}{{1+4{k^2}}}$��$��x_1^2=\frac{12}{{1+4{k^2}}}$����
��ȥx1��$\frac{��}{{{{��1+�ˣ�}^2}}}•\frac{{{{16}^2}{k^2}}}{{{{��1+4{k^2}��}^2}}}=\frac{12}{{1+4{k^2}}}$��
��$\frac{{{{��1+�ˣ�}^2}}}{��}=\frac{{{{16}^2}{k^2}��1+4{k^2}��}}{{12•{{��1+4{k^2}��}^2}}}$�������$��+\frac{1}{��}=\frac{64}{{3��\frac{1}{k^2}+4��}}-2$��
��$0��\frac{1}{k^2}��\frac{4}{3}$��$4��\frac{1}{k^2}+4��\frac{16}{3}$����$2��\frac{64}{{3��\frac{1}{k^2}+4��}}-2��\frac{10}{3}$��
��$2����+\frac{1}{��}��\frac{10}{3}$��0���ˣ�1��
��$f���ˣ�=��+\frac{1}{��}$����f���ˣ��ڣ�0��1����Ϊ����������$f��\frac{1}{3}��=\frac{10}{3}��f��1��=2$��
��$\frac{1}{3}���ˣ�1$��
�ۺϣ�1������2���ɵã��˵�ȡֵ��Χ��$\frac{1}{3}�ܦˣ�1$��
���� ���⿼����Բ���̵���������ֱ�ߺ�Բ����λ�ù�ϵ��Ӧ�ã�ѵ����ƽ�������ڽ����е�Ӧ�ã��������漰ֱ�ߺ�Բ���������еġ�������Ľ���˼�뷽�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1+\sqrt{5}}{2}$ | B�� | $\frac{1+\sqrt{3}}{2}$ | C�� | $\frac{4\sqrt{2}-2}{7}$ | D�� | $\frac{4\sqrt{2}+2}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
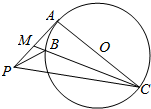 ����ͼ��ʾ��PAΪԲO�����ߣ��е�ΪA��AC��ֱ����MΪPA���е㣬MC��Բ���ڵ�B��
����ͼ��ʾ��PAΪԲO�����ߣ��е�ΪA��AC��ֱ����MΪPA���е㣬MC��Բ���ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com