
【题目】如图,已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 . 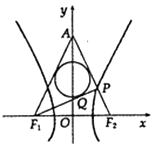
科目:高中数学 来源: 题型:
【题目】某商品在最近100天内的价格f(t)与时间t的函数关系式是

销售量g(t)与时间t的函数关系式是g(t)=-![]() +
+![]() (0≤t≤100),求这种商品的日销售额的最大值.
(0≤t≤100),求这种商品的日销售额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+![]() (a>1),
(a>1),
(1)判断函数f(x)在(-1,+∞)上的单调性,并证明你的判断;
(2)若a=3,求方程f(x)=0的正根(精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=1,且an+1= ![]() (n∈N*).
(n∈N*).
(1)证明:数列{ ![]() }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式;
(2)设bn=anan+1 , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺织厂订购一批棉花,其各种长度的纤维所占的比例如下表所示:

(1)请估计这批棉花纤维的平均长度与方差.
(2)如果规定这批棉花纤维的平均长度为4.90厘米,方差不超过1.200,两者允许误差均不超过0.10视为合格产品.请你估计这批棉花的质量是否合格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com