
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
科目:高中数学 来源: 题型:
【题目】随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:![]() ,2;
,2;![]() ,7;
,7;![]() ,10;
,10;![]() ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.

(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中![]() 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了准备里约奥运会的选拔,甲、乙两人进行队内射箭比赛,各射4支箭,两人4次所得环数如下:(最高为10环)
甲 | 6 | 6 | 9 | 9 |
乙 | 7 | 9 |
|
|
(Ⅰ)已知在乙的4支箭中随机选取1支时,此支射中环数小于6环的概率不为零,且在4支箭中,乙的平均环数高于甲的平均环数,求![]() 的值;
的值;
(Ⅱ)如果![]() ,
,![]() ,从甲、乙两人的4次比赛中随机各选取1次,并将其环数分别记为
,从甲、乙两人的4次比赛中随机各选取1次,并将其环数分别记为![]() ,
,![]() ,求
,求![]() 的概率;
的概率;
(Ⅲ)在4次比赛中,若甲、乙两人的平均环数相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形![]() 和矩形
和矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 与平面
与平面![]() 及平面
及平面![]() 所成的角分别为
所成的角分别为![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,且
的中点,且![]() .
.
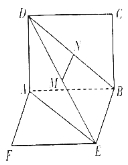
(1)求证:![]() 平面
平面![]() ;
;
(2)求线段![]() 的长;
的长;
(3)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行数学、物理、化学、生物四科竞赛,甲、乙、丙、丁分别参加其中的一科竞赛,且没有两人参加同一科竞赛.①甲没有参加数学生物竞赛;②乙没有参加化学、生物竞赛;③若甲参加化学竞赛,则丙不参加生物竞赛;④丁没有参加数学、化学竞赛;⑤丙没有参加数学、化学竞赛.若以上命题都是真命题,那么丁参加的竞赛科目是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=![]() AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
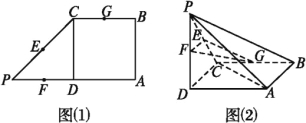
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)求在抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人 ,求至少抽到1名女生
的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有42名男生,30名女生,已知男女身高各有明显不同,现欲调查平均身高,若采用分层抽样方法,抽取男生1人,女生1人,这种做法是否合适,若不合适,应怎样抽取?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com