
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集为空集,求实数
的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2)![]()
【解析】试题分析:(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集(2)先根据绝对值定义将函数化为分段函数,求对应函数值域,即得f(x)﹣4的取值范围,根据倒数性质可得![]() 取值范围,最后根据方程解集为空集,确定实数
取值范围,最后根据方程解集为空集,确定实数![]() 的取值范围
的取值范围
试题解析:解:(1)解不等式|x﹣2|+|2x+1|>5,
x≥2时,x﹣2+2x+1>5,解得:x>2;
﹣![]() <x<2时,2﹣x+2x+1>5,无解,
<x<2时,2﹣x+2x+1>5,无解,
x≤﹣![]() 时,2﹣x﹣2x﹣1>5,解得:x<﹣
时,2﹣x﹣2x﹣1>5,解得:x<﹣![]() ,
,
故不等式的解集是(﹣∞,﹣![]() )∪(2,+∞);
)∪(2,+∞);
(2)f(x)=|x﹣2|+|2x+1|=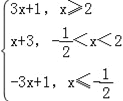 ,
,
故f(x)的最小值是![]() ,所以函数f(x)的值域为[
,所以函数f(x)的值域为[![]() ,+∞),
,+∞),
从而f(x)﹣4的取值范围是[﹣![]() ,+∞),
,+∞),
进而![]() 的取值范围是(﹣∞,﹣
的取值范围是(﹣∞,﹣![]() ]∪(0,+∞).
]∪(0,+∞).
根据已知关于x的方程![]() =a的解集为空集,所以实数a的取值范围是(﹣
=a的解集为空集,所以实数a的取值范围是(﹣![]() ,0].
,0].


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为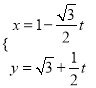 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
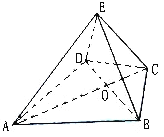
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为45°,求二面角
所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.
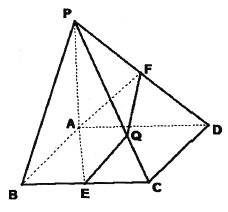
(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,设点
,设点![]() ,在
,在![]() 中,
中, ![]() ,周长为
,周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的一个动点,试根据
上的一个动点,试根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数,并说明理由.
存在的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了活跃元旦晚会气氛,主持人请12位同学做一个游戏,第一轮游戏中,主持人将标有数字1到12的十二张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字7到12的卡片的同学留下,其余的淘汰;第二轮将标有数字1到6的六张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字4到6的卡片的同学留下,其余的淘汰;第三轮将标有数字1,2,3的三张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字2,3的卡片的同学留下,其余的淘汰;第四轮用同样的办法淘汰一位同学,最后留下的这位同学获得一个奖品.已知同学甲参加了该游戏.
(1)求甲获得奖品的概率;
(2)设![]() 为甲参加游戏的轮数,求
为甲参加游戏的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com