
【题目】如图1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E、F分别是AB、CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF,如图2.
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB﹣ADGE=VD﹣GBCF时,求二面角D﹣BG﹣C平面角的余弦值.
【答案】
(1)
证明:∵点E、F分别是AB、CD的中点,
∴EF∥BC,又∠ABC=90°,∴AE⊥EF,
∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图建立空间坐标系E﹣xyz.
翻折前,连结AC交EF于点G,此时点G使得AG+GC最小.
EG= ![]() BC=2,又∵EA=EB=2.
BC=2,又∵EA=EB=2.
则A(0,0,2),B(2,0,0),C(2,4,0),
D(0,2,2),E(0,0,0),G(0,2,0),
∴ ![]() =(﹣2,2,2),
=(﹣2,2,2), ![]() =(﹣2,﹣2,0)
=(﹣2,﹣2,0)
∴ ![]() =(﹣2,2,2)(﹣2,﹣2,0)=0,
=(﹣2,2,2)(﹣2,﹣2,0)=0,
∴BD⊥CG.

(2)
解法一:设EG=k,∵AD∥平面EFCB,
∴点D到平面EFCB的距离为即为点A到平面EFCB的距离.
∵ ![]() [(3﹣k)+4]×2=7﹣k,
[(3﹣k)+4]×2=7﹣k,
∴ ![]() =
= ![]() ,
,
又 ![]() =
= ![]() ,
,
∵2VB﹣ADGE=VD﹣GBCF,∴ ![]() =
= ![]() ,
,
∴k=1即EG=1
设平面DBG的法向量为 ![]() ,∵G(0,1,0),
,∵G(0,1,0),
∴ ![]() ,
, ![]() =(﹣2,2,2),
=(﹣2,2,2),
则  ,即
,即 ![]()
取x=1,则y=2,z=﹣1,∴ ![]()
面BCG的一个法向量为 ![]()
则cos< ![]() >=
>= 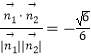
由于所求二面角D﹣BF﹣C的平面角为锐角,
所以此二面角平面角的余弦值为 ![]()
解法二:由解法一得EG=1,过点D作DH⊥EF,垂足H,
过点H作BG延长线的垂线垂足O,连接OD.
∵平面AEFD⊥平面EBCF,
∴DH⊥平面EBCF,∴OD⊥OB,
∴∠DOH就是所求的二面角D﹣BG﹣C的平面角.
由于HG=1,在△OHG中 ![]() ,
,
又DH=2,在△DOH中 ![]()
∴此二面角平面角的余弦值为 ![]() .
.


【解析】(1)由已知条件推导出AE⊥EF,AE⊥BE,BE⊥EF,建立空间坐标系E﹣xyz,利用向量法能求出BD⊥CG.(2)法一:设EG=k,由AD∥平面EFCB,得到点D到平面EFCB的距离为即为点A到平面EFCB的距离.分别求出平面DBG的法向量和面BCG的一个法向量,利用向量法能求出二面角平面角的余弦值.法二:由已知条件指法训练出EG=1,过点D作DH⊥EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD.由已知条件推导出∠DOH就是所求的二面角D﹣BG﹣C的平面角,由此能求出此二面角平面角的余弦值.
【考点精析】掌握平面与平面垂直的性质是解答本题的根本,需要知道两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() ,
, ![]() .
. ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点,
上一点,
(1)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,
,
求证: ![]() ∥平面
∥平面![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0,
=1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△
),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△ ![]() =
= ![]() .
.
(1)求点A的坐标;
(2)过点B(3,0)的直线l与椭圆E相交于点P、Q,直线AP、AQ分别与x轴相交于点M、N,点C( ![]() ,0),证明:|CM||CN|为定值,并求出该定值.
,0),证明:|CM||CN|为定值,并求出该定值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,
中,底面四边形ABCD是菱形, ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() .
.
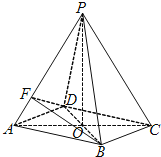
![]() Ⅰ
Ⅰ![]() 求证:
求证: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直线CP与平面BDF所成角的大小;
求直线CP与平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在线段PB上是否存在一点M,使得
在线段PB上是否存在一点M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=
(1)写出该函数的单调区间;
(2)若函数![]() =
=![]() -m恰有3个不同零点,求实数m的取值范围;
-m恰有3个不同零点,求实数m的取值范围;
(3)若![]() ≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com