
【题目】已知圆C:(x﹣1)2+y2=4
(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x﹣y+1=0与圆C交于A、B两点,求|AB|.
科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣4x﹣6y+m=0,若圆C与直线a:x+2y﹣3=0相交于M、N两点,且|MN|=2 ![]() .
.
(1)求m的值;
(2)是否存在直线l:x﹣y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围;若不存在,请说明理由.
,若存在,求出c的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某赛季甲、乙两名篮球运动员参加的每场比赛得分的茎叶图,由甲、乙两人这几场比赛得分的中位数之和是( ) 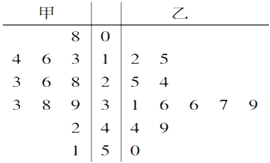
A.65
B.64
C.63
D.62
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据
房屋面积(平方米) | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出散点图
(2)求线性回归方程
(3)根据(2)的结果估计房屋面积为150平方米时的销售价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
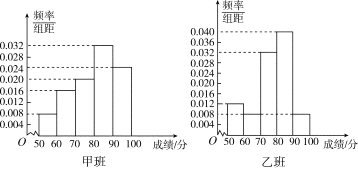
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为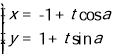 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P=![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com