
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
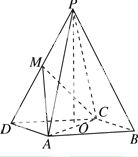
(1)证明:PB∥平面ACM;
(2)证明:AD⊥平面PAC.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为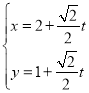 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有______
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏1 | 游戏2 | 游戏3 |
袋中装有一个红球和一个白球 | 袋中装有2个红球和2个白球 | 袋中装有3个红球和1个白球 |
取1个球, | 取1个球,再取1个球 | 取1个球,再取1个球 |
取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
A.游戏1B.游戏2C.游戏3D.游戏2和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:①“若x2+ y2 ≠0,则x,y不全为零”的否命题;②“正多边形都相似”的逆命题;③“若m>0,则x2+x-m=0有实根”的逆否命题;其中真命题的序号是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
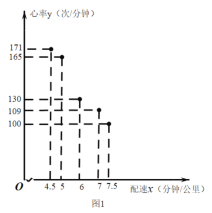
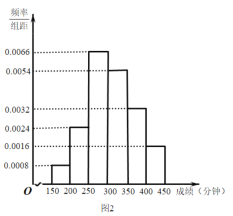
【题目】配速是马拉松运动中常使用的一个概念,是速度的一种,是指每公里所需要的时间,相比配速,把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率![]() (单位:次/分钟)和配速
(单位:次/分钟)和配速![]() (单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图:
(单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图:
(1)由散点图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)该跑者如果参加本次比赛,将心率控制在160左右跑完全程,估计他能获得的名次.
参考公式:线性回归方程![]() 中,
中,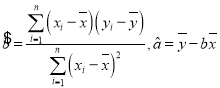 ,参考数据:
,参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com