
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c.已知 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若cosB= ![]() ,△ABC的周长为5,求b的长.
,△ABC的周长为5,求b的长.
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时,乘摩托艇以匀速vkm/h(8≤v≤40)从A港出发到距100km的B港去,然后乘汽车以匀速wkm/h(30≤w≤100)自B港向距300km的C市驶去.应该在同一天下午4至9点到达C市. 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh,yh.
(1)作图表示满足上述条件的x,y范围;
(2)如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)(元),那么v,w分别是多少时p最小?此时需花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,有下列三个命题:
,有下列三个命题:
①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() 、
、
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3.
,则k=﹣3.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为60°.
的夹角为60°.
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+y)=f(x)f(y),且f(1)= ![]() .
.
(1)当n∈N*时,求f(n)的表达式;
(2)设an=nf(n),n∈N* , 求证a1+a2+a3+…+an<2;
(3)设bn=(9﹣n) ![]() ,n∈N* , Sn为bn的前n项和,当Sn最大时,求n的值.
,n∈N* , Sn为bn的前n项和,当Sn最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
B.( ![]() ,1)
,1)
C.( ![]() )
)
D.(﹣∞,﹣ ![]() ,)
,) ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() (
(![]() ),从
),从![]() 上的点
上的点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,再从点
,再从点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() .设
.设![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: 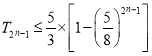 ;
;
(Ⅲ)若已知![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com