Question

1．实数x，y满足：$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ y≥\frac{1}{2}（x-3）\end{array}\right.$，则z=2x+y的最小值为（　　）

• A． 2
• B． 1
• C． $\frac{1}{2}$
• D． $\frac{1}{4}$

Answer 1

分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．

解答 解：由约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ y≥\frac{1}{2}（x-3）\end{array}\right.$作出可行域如图，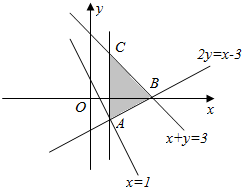

联立$\left\{\begin{array}{l}{x=1}\\{2y=x-3}\end{array}\right.$，解得A（1，-1），
化目标函数z=2x+y为y=-2x+z．
由图可知，当直线y=-2x+z过点A时，直线在y轴上的截距最小，z有最小值为2×1-1=1．
故选：B．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．