
如果项数均为
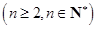 的两个数列
的两个数列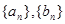 满足
满足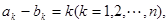 且集合
且集合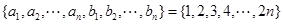 ,则称数列
,则称数列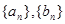 是一对“
是一对“ 项相关数列”.
项相关数列”.
(Ⅰ)设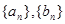 是一对“4项相关数列”,求
是一对“4项相关数列”,求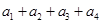 和
和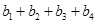 的值,并写出一对“
的值,并写出一对“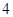 项
项
关数列”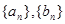 ;
;
(Ⅱ)是否存在“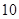 项相关数列”
项相关数列”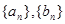 ?若存在,试写出一对
?若存在,试写出一对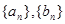 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)对于确定的 ,若存在“
,若存在“ 项相关数列”,试证明符合条件的“
项相关数列”,试证明符合条件的“ 项相关数列”有偶数对.
项相关数列”有偶数对.
(Ⅰ) ;
; ;
; :8,4,6,5;
:8,4,6,5; :7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.
:7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.
解析试题分析:(Ⅰ)依题意有,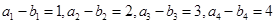 ,以及
,以及 ,求得
,求得 以及
以及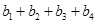 的值,写出符合条件的数列即可,答案不唯一;(Ⅱ)先假设存在,利用反证法证明得出矛盾,即可证明满足已知条件的“10项相关数列”不存在.依题意有
的值,写出符合条件的数列即可,答案不唯一;(Ⅱ)先假设存在,利用反证法证明得出矛盾,即可证明满足已知条件的“10项相关数列”不存在.依题意有 ,以及
,以及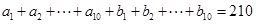 成立,解出
成立,解出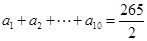 与已知矛盾,即证;(Ⅲ)对于确定的
与已知矛盾,即证;(Ⅲ)对于确定的 ,任取一对“
,任取一对“ 项相关数列”
项相关数列”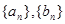 ,构造新数对
,构造新数对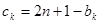 ,
,
 ,则可证明新数对也是“
,则可证明新数对也是“ 项相关数列”,但是数列
项相关数列”,但是数列 与
与 是不同的数列,可知“
是不同的数列,可知“ 项相关数列”都是成对对应出现的,即符合条件的 “
项相关数列”都是成对对应出现的,即符合条件的 “ 项相关数列”有偶数对.
项相关数列”有偶数对.
试题解析:(Ⅰ)依题意,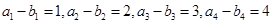 ,相加得,
,相加得, ,又
,又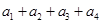
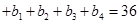 ,
,
则 ,
,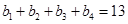 .
.
“4项相关数列” :8,4,6,5;
:8,4,6,5; :7,2,3,1(不唯一) 4分
:7,2,3,1(不唯一) 4分
(Ⅱ)不存在.
理由如下:假设存在“10项相关数列”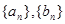 ,
,
则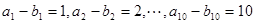 ,
,
相加得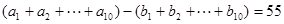 .
.
又由已知 ,
,
所以 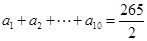 ,显然不可能,所以假设不成立.
,显然不可能,所以假设不成立.
从而不存在 “10项相关数列”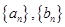 . 8分
. 8分
(Ⅲ)对于确定的 ,任取一对 “
,任取一对 “ 项相关数列”
项相关数列”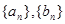 ,
,
令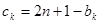 ,
,
 ,
,
(先证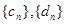 也必为 “
也必为 “ 项相关数列”)
项相关数列”)
因为
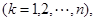
又因为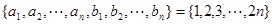 ,
,
很显然有
 ,
,
所以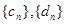 也必为 “
也必为 “ 项相关数列”.
项相关数列”.
(再证数列 与
与 是不同的数列)
是不同的数列)
假设 与
与 相同,则
相同,则 的第二项
的第二项 ,又
,又 ,则
,则 ,即
,即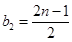 ,显然矛盾.
,显然矛盾.
从而,符合条件的 “ 项相关数列”有偶数对. 13分
项相关数列”有偶数对. 13分
考点:1.等差数列的前 项和公式;2.反证法及其应用
项和公式;2.反证法及其应用


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com