
【题目】设![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是AB的垂直平分线,
是AB的垂直平分线,
(1)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(2)若![]() ,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上关于
是抛物线上关于![]() 轴对称的两点,点
轴对称的两点,点![]() 是抛物线准线
是抛物线准线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求抛物线的方程;
(2)若![]() 为抛物线上异于原点的任意一点,过
为抛物线上异于原点的任意一点,过![]() 作
作![]() 的垂线交准线
的垂线交准线![]() 于点
于点![]() ,则直线
,则直线![]() 与抛物线是何种位置关系?请说明理由.
与抛物线是何种位置关系?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)阅读以下案例,利用此案例的想法化简![]() .
.
案例:考察恒等式![]() 左右两边
左右两边![]() 的系数.
的系数.
因为右边![]() ,
,
所以,右边![]() 的系数为
的系数为![]() ,
,
而左边![]() 的系数为
的系数为![]() ,
,
所以![]() =
=![]() .
.
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
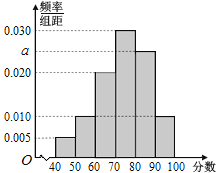
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问在
两点,试问在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?若存在,求出定点
恒成立?若存在,求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两位同学上学期间,每天7:30之前到校的概率均为![]() .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用![]() 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量![]() 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个地区计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水的年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过12的概率;
(2)若水的年入流量![]() 与其蕴含的能量
与其蕴含的能量![]() (单位:百亿万焦)之间的部分对应数据为如下表所示:
(单位:百亿万焦)之间的部分对应数据为如下表所示:
年入流量 | 6 | 8 | 10 | 12 | 14 |
蕴含的能量 | 1.5 | 2.5 | 3.5 | 5 | 7.5 |
用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(回归方程系数用分数表示)
;(回归方程系数用分数表示)
(3)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
附:回归方程系数公式: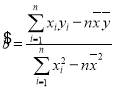 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com