
【题目】已知函数f(x)=axex , 其中常数a≠0,e为自然对数的底数. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a=1时,求函数f(x)的极值;
(Ⅲ)若直线y=e(x﹣ ![]() )是曲线y=f(x)的切线,求实数a的值.
)是曲线y=f(x)的切线,求实数a的值.
【答案】解:(Ⅰ)函数的导数f′(x)=a(ex+xex)=a(1+x)ex , 若a>0,由f′(x)>0得x>﹣1,即函数的单调递增区间为(﹣1,+∞),
由f′(x)<0,得x<﹣1,即函数的单调递减区间为(﹣∞,﹣1),
若a<0,由f′(x)>0得x<﹣1,即函数的单调递增区间为(﹣∞,﹣1),
由f′(x)<0,得x>﹣1,即函数的单调递减区间为(﹣1,+∞);
(Ⅱ)当a=1时,由(1)得函数的单调递增区间为(﹣1,+∞),函数的单调递减区间为(﹣∞,﹣1),
即当x=﹣1时,函数f(x)取得极大值为f(﹣1)=﹣ ![]() ,无极小值;
,无极小值;
(Ⅲ)设切点为(m,amem),
则对应的切线斜率k=f′(m)=a(1+m)em ,
则切线方程为y﹣amem=a(1+m)em(x﹣m),
即y=a(1+m)em(x﹣m)+amem=a(1+m)emx﹣ma(1+m)em+amem=a(1+m)emx﹣m2aem ,
∵y=e(x﹣ ![]() )=y=ex﹣
)=y=ex﹣ ![]() e,
e,
∴ 
∴ ![]() ,
,
即若直线y=e(x﹣ ![]() )是曲线y=f(x)的切线,则实数a的值是
)是曲线y=f(x)的切线,则实数a的值是 ![]()
【解析】(Ⅰ)求函数的导数,根据函数单调性和导数之间的关系即可求函数f(x)的单调区间;(Ⅱ)当a=1时,根据函数极值和导数之间的关系即可求函数f(x)的极值;(Ⅲ)设出切点坐标为(m,amem),求出切线斜率和方程,根据导数的几何意义建立方程关系即可求实数a的值.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101﹣150为轻度污染;151﹣200为中度污染;201~300为重度污染;>300为严重污染. 一环保人士记录去年某地某月10天的AQI的茎叶图如图.
(Ⅰ)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共30天)
(Ⅱ)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为ξ,求ξ的概率分布列和数学期望.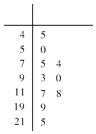
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣m|﹣|x+3m|(m>0). (Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)对于任意实数x,t,不等式f(x)<|2+t|+|t﹣1|恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,点
,点![]() .
.
(Ⅰ)经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() .
.
(Ⅱ)问是否存在直线![]() 与椭圆交于两点
与椭圆交于两点![]() 、
、![]() 且
且![]() ,若存在,求出直线
,若存在,求出直线![]() 斜率的取值范围;若不存在说明理由.
斜率的取值范围;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),离心率e=
=1(a>b>0),离心率e= ![]() ,已知点P(0,
,已知点P(0, ![]() )到椭圆C的右焦点F的距离是
)到椭圆C的右焦点F的距离是 ![]() .设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
.设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)求点Q的横坐标x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
若函数f(x)=log2(x2﹣ax+3a)在[2,+∞)上是增函数,则x2﹣ax+3a>0且f(2)>0,根据二次函数的单调性,我们可得到关于a的不等式,解不等式即可得到a的取值范围.
若函数f(x)=log2(x2﹣ax+3a)在[2,+∞)上是增函数,
则当x∈[2,+∞)时,
x2﹣ax+3a>0且函数f(x)=x2﹣ax+3a为增函数
即![]() ,f(2)=4+a>0
,f(2)=4+a>0
解得﹣4<a≤4
故选:C.
【点睛】
本题考查的知识点是复合函数的单调性,二次函数的性质,对数函数的单调区间,其中根据复合函数的单调性,构造关于a的不等式,是解答本题的关键.
【题型】单选题
【结束】
10
【题目】圆锥的高![]() 和底面半径
和底面半径![]() 之比
之比![]() ,且圆锥的体积
,且圆锥的体积![]() ,则圆锥的表面积为( )
,则圆锥的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x-4| (x∈R)
(1)用分段形式写出函数f(x)的表达式,并作出函数f(x)的图象;
(2) 根据图象指出f(x)的单调区间,并写出不等式f(x)>0的解集;
(3) 若h(x)=f(x)-k有三个零点,写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com