
【题目】已知椭圆 ![]() =1(a>b>0)经过点(0,
=1(a>b>0)经过点(0, ![]() ),离心率为
),离心率为 ![]() ,左右焦点分别为F1(﹣c,0),F2(c,0).
,左右焦点分别为F1(﹣c,0),F2(c,0).
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l:y=﹣ ![]() x+m与椭圆交于A、B两点,与以F1F2为直径的圆交于C、D两点,且满足
x+m与椭圆交于A、B两点,与以F1F2为直径的圆交于C、D两点,且满足 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.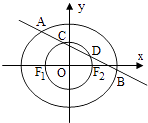
【答案】解:(Ⅰ)由题意可得 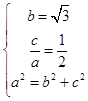 ,
,
解得 ![]() ,c=1,a=2.
,c=1,a=2.
∴椭圆的方程为 ![]() .
.
(Ⅱ)由题意可得以F1F2为直径的圆的方程为x2+y2=1.
∴圆心到直线l的距离d= ![]() ,
,
由d<1,可得 ![]() .(*)
.(*)
∴|CD|=2 ![]() =
= ![]() =
= ![]() .
.
设A(x1 , y1),B(x2 , y2).
联立 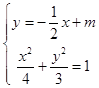 ,
,
化为x2﹣mx+m2﹣3=0,
可得x1+x2=m, ![]() .
.
∴|AB|=  =
= ![]() .
.
由 ![]() =
= ![]() ,得
,得 ![]() ,
,
解得 ![]() 满足(*).
满足(*).
因此直线l的方程为 ![]()
【解析】(Ⅰ)由题意可得 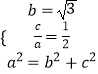 ,解出即可.(Ⅱ)由题意可得以F1F2为直径的圆的方程为x2+y2=1.利用点到直线的距离公式可得:圆心到直线l的距离d及d<1,可得m的取值范围.利用弦长公式可得|CD|=2
,解出即可.(Ⅱ)由题意可得以F1F2为直径的圆的方程为x2+y2=1.利用点到直线的距离公式可得:圆心到直线l的距离d及d<1,可得m的取值范围.利用弦长公式可得|CD|=2 ![]() .设A(x1 , y1),B(x2 , y2).把直线l的方程与椭圆的方程联立可得根与系数的关系,进而得到弦长|AB|=
.设A(x1 , y1),B(x2 , y2).把直线l的方程与椭圆的方程联立可得根与系数的关系,进而得到弦长|AB|= ![]() .由
.由 ![]() =
= ![]() ,即可解得m.
,即可解得m.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an},{bn}的通项公式.
(2)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个动点P在圆x2+y2=36上移动,它与定点Q(4,0)所连线段的中点为M.
(1)求点M的轨迹方程.
(2)过定点(0,﹣3)的直线l与点M的轨迹交于不同的两点A(x1 , y1),B(x2 , y2)且满足 ![]() +
+ ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是AB=2,BC= ![]() 的矩形,△PAB是等边三角形,侧面PAB⊥底面ABCD
的矩形,△PAB是等边三角形,侧面PAB⊥底面ABCD
(Ⅰ)证明:BC⊥面PAB
(Ⅱ)求侧棱PC与底面ABCD所成的角.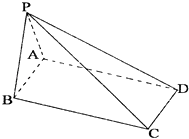
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1 , 点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( ) 
A.2:1
B.3:1
C.3:2
D.4:3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式|x﹣2|+|x+2|>m的解集是R; q:关于x的不等式x2+mx+4>0的解集是R.则p成立是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.即不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1+a5=17.
(1)若{an}还同时满足: ①{an}为等比数列;②a2a4=16;③对任意的正整数n,a2n<a2n+2 , 试求数列{an}的通项公式.
(2)若{an}为等差数列,且S8=56. ①求该等差数列的公差d;②设数列{bn}满足bn=3nan , 则当n为何值时,bn最大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com