
【题目】在古代三国时期吴国的数学家赵爽创制了一幅“赵爽弦图”,由四个全等的直角三角形围成一个大正方形,中间空出一个小正方形(如图阴影部分)。若直角三角形中较小的锐角为a。现向大正方形区城内随机投掷一枚飞镖,要使飞镖落在小正方形内的概率为![]() ,则
,则![]() _____________。
_____________。

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某地新建一家服装厂,从今年7月份开始投产,并且前4个月的产量分别为![]() 万件、
万件、![]() 万件、
万件、![]() 万件、
万件、![]() 万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:
万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:![]() ,
,![]() ,
,![]() ,
,![]() .你将利用零一种模型去估算以后几个月的产量?
.你将利用零一种模型去估算以后几个月的产量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的基本规则是:①“盲拍”,即所有参与竞拍的人都要网络报价一次,每个人不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞拍人的出价从高到低分配名额.某人拟参加![]() 年
年![]() 月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的数据,统计了最近
月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的数据,统计了最近![]() 个月参与竞拍的人数(见下表):
个月参与竞拍的人数(见下表):
月份 |
|
|
|
|
|
月份编号 |
|
|
|
|
|
竞拍人数 |
|
|
|
|
|
(1)由收集数据的散点图发现,可用线性回归模型拟合竞拍人数![]() (万人)与月份编号
(万人)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:![]() ,并预测
,并预测![]() 年
年![]() 月份参与竞拍的人数.
月份参与竞拍的人数.
(2)某市场调研机构从拟参加![]() 年
年![]() 月份车牌竞拍人员中,随机抽取了
月份车牌竞拍人员中,随机抽取了![]() 人,对他们的拟报价价格进行了调查,得到如下频数分布表和频率分布直方图:
人,对他们的拟报价价格进行了调查,得到如下频数分布表和频率分布直方图:
报价区间(万元) |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(i)求![]() 、
、![]() 的值及这
的值及这![]() 位竞拍人员中报价大于
位竞拍人员中报价大于![]() 万元的概率;
万元的概率;
(ii)若![]() 年
年![]() 月份车牌配额数量为
月份车牌配额数量为![]() ,假设竞拍报价在各区间分布是均匀的,请你根据以上抽样的数据信息,预测(需说明理由)竞拍的最低成交价.
,假设竞拍报价在各区间分布是均匀的,请你根据以上抽样的数据信息,预测(需说明理由)竞拍的最低成交价.
参考公式及数据:①回归方程![]() ,其中
,其中 ,
,![]() ;
;
②![]() ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:

(1)求频率直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中人选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(ax2+x+6).
(1)若a=﹣1,求f(x)的定义域,并讨论f(x)的单调性;
(2)若函数f(x)的定义域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线顶点在原点,焦点在x轴上,且过点(4,4),焦点为F.
(1)求抛物线的焦点坐标和标准方程;
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中作截面PQR,若PQ与CB的延长线交于点M,RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
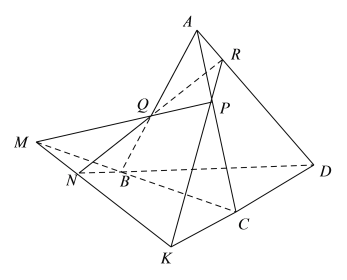
(1)求证:直线![]() 平面PQR;
平面PQR;
(2)求证:点K在直线MN上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com