Question

若不等式|ax+2|＜6的解是（-1，2）；则实数a=________．

Answer 1

-4
分析：先根据绝对值不等式的解法，将原不等式等价转化为一次不等式，再对a分类讨论，求出a的值即可．
解答：∵|ax+2|＜6，∴-6＜ax+2＜6，-8＜ax＜4
①当a=0时，原不等式的解集为R，与题设不符（舍去），
②当a＞0时，有 ，
而已知原不等式的解集为（-1，2），所以有：
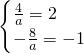
．此方程无解（舍去）．
③当a＜0时，有 ，
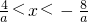
所以有
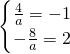
解得a=-4，
故答案为：-4．
点评：本小题主要考查绝对值不等式的解法、等式的解法等基础知识，考查运算求解能力，考查考查分类讨论思想．属于基础题．