
【题目】已知等比数列{an}满足 ![]() ,n∈N* . (Ⅰ)求数列{an}的通项公式;
,n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 若不等式Sn>kan﹣2对一切n∈N*恒成立,求实数k的取值范围.
【答案】解:(Ⅰ)设等比数列{an}的公比为q, ∵ ![]() ,n∈N* , ∴a2+a1=9,a3+a2=18,
,n∈N* , ∴a2+a1=9,a3+a2=18,
∴ ![]() ,
,
又2a1+a1=9,∴a1=3.
∴ ![]() .
.
(Ⅱ) ![]() ,
,
∴3(2n﹣1)>k32n﹣1﹣2,∴ ![]() .
.
令 ![]() ,f(n)随n的增大而增大,
,f(n)随n的增大而增大,
∴ ![]() .∴
.∴ ![]() .
.
∴实数k的取值范围为 ![]()
【解析】(Ⅰ)利用等比数列{an}满足 ![]() ,确定数列的公比与首项,即可求数列{an}的通项公式;(Ⅱ)求出Sn , 再利用不等式Sn>kan﹣2,分离参数,求最值,即可求实数k的取值范围.
,确定数列的公比与首项,即可求数列{an}的通项公式;(Ⅱ)求出Sn , 再利用不等式Sn>kan﹣2,分离参数,求最值,即可求实数k的取值范围.
【考点精析】根据题目的已知条件,利用数列的通项公式的相关知识可以得到问题的答案,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】已知![]() 是方程
是方程![]()
![]() 的两个不等实根,函数
的两个不等实根,函数![]() 的定义域为
的定义域为![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最值;
的最值;
(2)试判断函数![]() 在区间
在区间![]() 的单调性;
的单调性;
(3)设![]() ,试证明:对于
,试证明:对于![]() ,若
,若![]() ,则
,则 .
.
(参考公式: ![]() ,当且仅当
,当且仅当![]() 时等号成立)
时等号成立)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,A(1,3),BC边所在的直线方程为y﹣1=0,AB边上的中线所在的直线方程为x﹣3y+4=0. (Ⅰ)求B,C点的坐标;
(Ⅱ)求△ABC的外接圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}和{bn}(bn≠0,n∈N*),满足a1=b1=1,anbn+1﹣an+1bn+bn+1bn=0
(1)令cn= ![]() ,证明数列{cn}是等差数列,并求{cn}的通项公式
,证明数列{cn}是等差数列,并求{cn}的通项公式
(2)若bn=2n﹣1 , 求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求y关于x的线性回归方程 ![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式: ![]() =
= 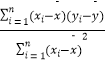 =
= 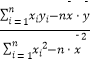 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的展开式各项系数和为M,
的展开式各项系数和为M, ![]() 的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求
的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求 ![]() 的展开式中:
的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车,购车费用是10万元,每年使用的保险费、养路费、汽车费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元,问这种汽车使用多少年时,它的平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]()
x | |||||
2x+ | |||||
sin(2x+ | |||||
f(x) |

(1)用五点法完成下列表格,并画出函数f(x)在区间 ![]() 上的简图;
上的简图;
(2)若 ![]() ,函数g(x)=f(x)+m的最小值为2,试求处函数g(x)的最大值,指出x取值时,函数g(x)取得最大值.
,函数g(x)=f(x)+m的最小值为2,试求处函数g(x)的最大值,指出x取值时,函数g(x)取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com