
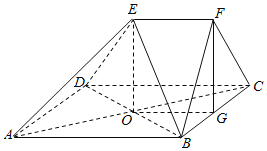
【题目】如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF![]() AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:
AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:

(1)OG∥平面ABFE;
(2)AC⊥平面BDE.
【答案】(1)见解析(2)见解析
【解析】
(1)根据中位线的性质证明OG∥AB后即可得证;
(2)连接FG、EO,由题意EO⊥平面ABCD,可得EO⊥AC,由线面垂直的判定即可得解.
证明:(1)∵四边形ABCD是菱形,AC,BD相交于点O,
∴O是AC中点,
∵G为BC的中点,∴OG∥AB,
∵OG平面ABFE,AB平面ABFE,
∴OG∥平面ABFE.
(2)连接FG、EO,
∵四边形ABCD是菱形,AC,BD相交于点O,
∴AC⊥BD,O是AC中点,
∵G为BC的中点,∵EF∥AB,EF![]() AB,平面BCF⊥平面ABCD,BF=CF,
AB,平面BCF⊥平面ABCD,BF=CF,
∴FG⊥平面ABCD,∴EO⊥平面ABCD,∴EO⊥AC,
∵EO∩BD=O,∴AC⊥平面BDE.


科目:高中数学 来源: 题型:
【题目】网购已经成为一种新型的购物方式,2018年天猫双11,仅1小时47分钟成交额超过1000亿元,比2017年达到1000亿元的时间缩短了7个小时,为了研究市民对网购的依赖性,从A城市16﹣59岁人群中抽取一个容量为100的样本,得出下列2×2列联表,其中16﹣39岁为青年,40﹣59岁为中年,当日消费金额超过1000元为消费依赖网购,否则为消费不依赖网购.
依赖网购 | 不依赖网购 | 小计 | |
青年(16﹣39岁) | 40 | 20 | |
中年(40﹣59岁) | 20 | 20 | |
小计 |
(1)完成2×2列联表,计算X2值,并判断是否有95%的把握认为网购依赖和年龄有关?
(2)把样本中的频率当作概率,随机从A城市中选取5人,其中依赖网购的人数为随机变量X,求随机变量X的分布列及期望(附:X2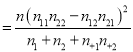 ,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率e
1(a>b>0)的离心率e![]() ,且点P(
,且点P(![]() ,1)在椭圆C上.
,1)在椭圆C上.
(1)求椭圆C的方程;
(2)若椭圆C的左焦点为F,右顶点为A,点M(s,t)(t>0)是椭圆C上的动点,直线AM与y轴交于点D,点E是y轴上一点,EF⊥DF,EA与椭圆C交于点G,若△AMG的面积为2![]() ,求直线AM的方程.
,求直线AM的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com