
【题目】一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价![]() (元)与销量
(元)与销量![]() (杯)的相关数据如下表:
(杯)的相关数据如下表:
单价 | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量 | 120 | 110 | 90 | 70 | 60 |
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)
附:线性回归方程![]() 中斜率和截距最小二乗法估计计算公式:
中斜率和截距最小二乗法估计计算公式: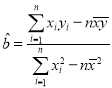 ,
,![]() ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
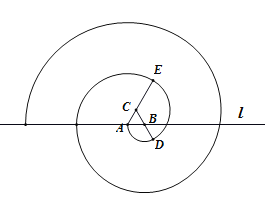
【题目】原始的蚊香出现在宋代.根据宋代冒苏轼之名编写的《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线![]() 上取长度为1的线段
上取长度为1的线段![]() ,做一个等边三角形
,做一个等边三角形![]() ,然后以点
,然后以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,以此类推,当得到的“螺旋蚊香”与直线
,以此类推,当得到的“螺旋蚊香”与直线![]() 恰有
恰有![]() 个交点时,“螺旋蚊香”的总长度的最小值为( )
个交点时,“螺旋蚊香”的总长度的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆O的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上异于A,B两点的一个动点,以点P为直角顶点作等腰直角![]() ,且点D与圆心O分布在PC的两侧,设
,且点D与圆心O分布在PC的两侧,设![]() .
.
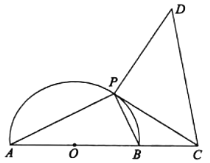
(1)把线段PC的长表示为![]() 的函数;
的函数;
(2)求四边形ACDP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2+pn,且a4,a7,a12成等比数列.
(1)求数列{an}的通项公式;
(2)若bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
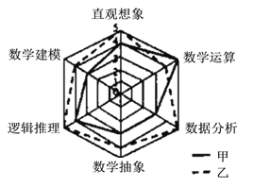
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是无穷数列,若存在正整数k,使得对任意
是无穷数列,若存在正整数k,使得对任意![]() ,均有
,均有![]() ,则称
,则称![]() 是间隔递增数列,k是
是间隔递增数列,k是![]() 的间隔数,下列说法正确的是( )
的间隔数,下列说法正确的是( )
A.公比大于1的等比数列一定是间隔递增数列
B.已知![]() ,则
,则![]() 是间隔递增数列
是间隔递增数列
C.已知![]() ,则
,则![]() 是间隔递增数列且最小间隔数是2
是间隔递增数列且最小间隔数是2
D.已知![]() ,若
,若![]() 是间隔递增数列且最小间隔数是3,则
是间隔递增数列且最小间隔数是3,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com