
【题目】某位同学在2015年5月进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了5月1日至5月5日的白天平均气温x(°C)与该奶茶店的这种饮料销量y(杯),得到如下数据:
日 期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据不是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
(参考公式: ![]() =
= 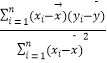 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
【答案】
(1)解:设“选取的2组数据不是相邻2天数据”为事件A
所有基本事件(m,n)(其中m,n为5月份的日期数)有:
(1,2),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4),(3,5),(4,5)共10种;
事件A包括的基本事件有
(1,3),(1,4),(1,5),(2,4),(2,5),(3,5)共6种;
所以P(A)= ![]() ;
;
(2)解:由数据,求得 ![]() =
= ![]() =10,
=10,
![]() =
= ![]() =25;
=25;
![]() =
= ![]() =2.1,
=2.1,
![]() =
= ![]() ﹣
﹣ ![]()
![]() =4,
=4,
∴y关于x的线性回归方程为 ![]() =2.1x+4
=2.1x+4
【解析】(1)利用列举法求出“选取的2组数据不是相邻2天数据”的基本事件数,求出对应的概率即可;(2)根据题目中的数据,利用公式求出平均数 ![]() 、
、 ![]() 与回归系数
与回归系数 ![]() 、
、 ![]() ,写出线性回归方程.
,写出线性回归方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且经过点A(0,﹣1).
,且经过点A(0,﹣1).
(1)求椭圆C的标准方程;
(2)如果过点 ![]() 的直线与椭圆交于M,N两点(M,N点与A点不重合),求证:△AMN为直角三角形.
的直线与椭圆交于M,N两点(M,N点与A点不重合),求证:△AMN为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对边的边长分别为a,b,c,给出下列四个结论: ①以 ![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以 ![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以a2 , b2 , c2为边长的三角形一定存在;
④以 ![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
那么,正确结论的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位同学家里订了一份报纸,送报人每天都在在早上5:20~6:40之间将报纸送到达,该同学的爸爸需要早上6:00~7:00之间出发去上班,则这位同学的爸爸在离开家前能拿到报纸的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1 , 若 ![]() =x
=x ![]() +y
+y ![]() +z
+z ![]() ,则(x,y,z)为( )
,则(x,y,z)为( )
A.( ![]() ,
, ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 |
y | ﹣6 | 0 | 4 | 6 | 6 | 4 | 0 | ﹣6 |
则一元二次不等式ax2+bx+c>0的解集是( )
A.{x|x<﹣2,或x>3}
B.{x|x≤﹣2,或x≥3}
C.{x|﹣2<x<3}
D.{x|﹣2≤x≤3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
(1)求证:PE⊥AD;
(2)若CA=CB,求证:平面PEC⊥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com