
【题目】在平面直角坐标系中,已知圆心![]() 在直线
在直线![]() 上的圆
上的圆![]() 经过点
经过点![]() ,但不经过坐标原点,并且直线
,但不经过坐标原点,并且直线![]() 与圆
与圆![]() 相交所得的弦长为4.
相交所得的弦长为4.
(1)求圆![]() 的一般方程;
的一般方程;
(2)若从点![]() 发出的光线经过
发出的光线经过![]() 轴反射,反射光线刚好通过圆
轴反射,反射光线刚好通过圆![]() 的圆心,求反射光线所在的直线方程(用一般式表达).
的圆心,求反射光线所在的直线方程(用一般式表达).
【答案】(1)![]() ;(2)反射光线所在的直线方程的一般式为:
;(2)反射光线所在的直线方程的一般式为: ![]() .
.
【解析】试题分析:(1)设圆![]() ,根据圆心
,根据圆心![]() 在直线
在直线![]() 上,圆
上,圆![]() 经过点
经过点![]() ,并且直线
,并且直线![]() 与圆
与圆![]() 相交所得的弦长为
相交所得的弦长为![]() ,列出关于
,列出关于![]() 的方程组,解出
的方程组,解出![]() 的值,可得圆的标准方程,再化为一般方程即可;(2)点
的值,可得圆的标准方程,再化为一般方程即可;(2)点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,反射光线所在的直线即为
,反射光线所在的直线即为![]() ,又因为
,又因为![]() ,
,
利用两点式可得反射光线所在的直线方程,再化为一般式即可.
试题解析:(1)设圆![]() ,
,
因为圆心![]() 在直线
在直线![]() 上,所以有:
上,所以有: ![]() ,
,
又因为圆![]() 经过点
经过点![]() ,所以有:
,所以有: ![]() ,
,
而圆心到直线![]() 的距离为
的距离为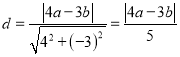 ,
,
由弦长为4,我们有弦心距![]() .
.
所以有![]()
联立成方程组解得: 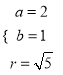 或
或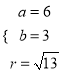 ,
,
又因为![]() 通过了坐标原点,所以
通过了坐标原点,所以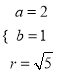 舍去.
舍去.
所以所求圆的方程为: ![]() ,
,
化为一般方程为: ![]() .
.
(2)点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
反射光线所在的直线即为![]() ,又因为
,又因为![]() ,
,
所以反射光线所在的直线方程为: ![]() ,
,
所以反射光线所在的直线方程的一般式为: ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对正整数n,记In={1,2,3,...,n},Pn={![]() |m∈In,k∈In}.
|m∈In,k∈In}.
(1)求集合P7中元素的个数;
(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pn能分成两个不相交的稀疏集的并集.
查看答案和解析>>
科目:高中数学 来源: 题型:
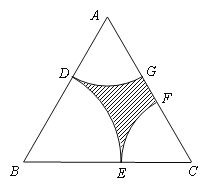
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布图中![]() 的值,并估计该企业的职工对该部门评分不低于80的概率;
的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率..
的概率..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是A1B1上一点,若平面EBD与平面ABCD所成锐二面角的正切值为 ![]() ,设三棱锥A﹣A1D1E外接球的直径为a,则
,设三棱锥A﹣A1D1E外接球的直径为a,则 ![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com