
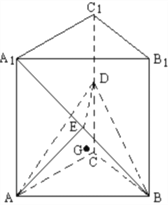
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,D、E分别是
,D、E分别是![]() 与
与![]() 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是![]() 的重心
的重心![]()
(Ⅰ)求![]() 与平面ABD所成角的余弦值
与平面ABD所成角的余弦值
(Ⅱ)求点![]() 到平面
到平面![]() 的距离
的距离
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若x2>1,则x>1”的否命题为“若x2>1,则![]() ”
”
B.命题“?![]() ,x>1”的否定是“
,x>1”的否定是“![]() ,x2>1”
,x2>1”
C.命题“若x=y,则cosx=cosy"的逆否命题为假命题
D.命题“若x=y,则cosx=cosy"的逆命题为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2x-![]() .
.
(Ⅰ)若f(x)=![]() ,求x的值;
,求x的值;
(Ⅱ)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(I)求Z的分布列和均值;
(II)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过圆O1、圆O2交点的直线的直角坐标方程
查看答案和解析>>
科目:高中数学 来源: 题型:
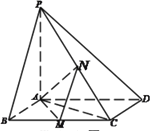
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明: ![]() ;
;
(2)若![]() 为
为![]() 的中点时,
的中点时,![]() 与平面
与平面![]() 所成的角最大,且所成角的正切值为
所成的角最大,且所成角的正切值为![]() ,求点A到平面
,求点A到平面![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的外接圆半径
的外接圆半径![]() ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且![]() .
.
(I)求角B和边长b;
(II)求![]() 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线l的参数方程为 (t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=4cosθ.
(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=4cosθ.
(1)写出直线l的普通方程和圆C的直角坐标方程.
(2)若点P坐标为(1,1),圆C与直线l交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com